А. Генеральная совокупность с двумя признаками.

Для генеральной совокупности с двумя признаками определяются следующие пять параметров (два математических ожидания, две дисперсии, один коэффициент парной корреляции):

1. Математическое ожидание х: Mx=μx

2. Математическое ожидание у: My=μy

3. Дисперсия х: Dx=σ2x

4. Дисперсия у: Dy=σ2y

5. Коэффициент парной корреляции:

Квадрат коэффициента корреляции называют коэффициентом детерминации.

а) Проверка значимости параметров связи

Значимость коэффициента корреляции показывает зависимость или независимость признаков.

Если коэффициент незначим, то признаки x и y считаются независимыми.

Проверяется гипотеза Н0: r = 0. Для этого вычисляется tнабл и находится tтабл по таблице t– распределения Стьюдента

tтабл. находится для определенного значения a (a=10%, 5%, 2%, 1%) и n=n-2

Если çtнабл.ç>tтабл., то гипотеза H0 отвергается с вероятностью ошибки a.

Если çtнабл.ç≤tтабл, то гипотеза не отвергается

при n>100 или

б) Интервальная оценка параметров связи

Интервальные оценки обычно находят для значимых параметров связи.

Находим значение статистики Z по формуле

.

Находим точность интервальной оценки по формуле

(t¡ – находится по таблице t-распределения для заданного g)

Интервальная оценка для MZ имеет вид

.

С помощью обратной функции получаем интервальную оценку коэффициента корреляции r (используется таблица Фишера-Иейтса)

Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля (с тем же уровнем a).

Интервальные оценки для коэффициента регрессии получают по формулам:

;

,

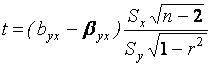где t имеет распределение Стьюдента с n=n-2 степенями свободы.

Примечание. Для значимого коэффициента корреляции некоторые авторы рекомендуют оценку r при небольших выборках

или

для

Регрессионный анализ

Регрессионный анализ используется после того, как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты.

Регрессионным анализом называется метод статистического анализа зависимости случайной величины у от переменных , рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения xj.

Предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием ỹ, являющимся функцией от аргументов xj и постоянной, не зависящей от аргументов дисперсий s2.

Наиболее часто встречаются следующие виды уравнений регрессии:

‑ линейное многомерное

‑ полином

‑ гипербола

‑ степенное

Полиномиальное, гиперболическое и степенное уравнения приводятся к линейному.

А. Простейшее линейное уравнение регрессии.

а) Оценка уравнения регрессии.

Предполагаем, что в «среднем» у есть линейная функция от х, т.е. уравнение регрессии имеет вид:

,

где ‑ условное математическое ожидание М(у/х);

‑ коэффициенты, которые необходимо оценить по результатам выборочных наблюдений.

Оценить ‑ это значит найти их оценки по выборке (оценки обозначают как в0 и в1). Говорят, что имеем оценку уравнения, т.е. в0 и в1 – найденны, например, методом наименьших квадратов.

Оценка уравнения регрессии записывается в виде:

б) Определение интервальной оценки

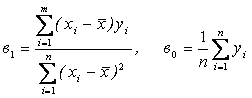
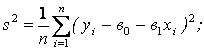
где в0 – оценка b0, т.е. Мв0 =b0;

tg ‑ t распределение для уровня значимости a=1-g и числа степеней свободы

v=n-2

в) Проверка значимости b1 (значимости уравнения регрессии)

проверяется гипотеза о равенстве нулю b1 при альтернативной гипотезе

H0: b1=0

H1: b1¹0

Гипотеза H0: b1=0 отвергается с вероятностью ошибки a при выполнении неравенства | t1 |>tкр (a, g=n-2) и уравнение регрессии считается значимым

где ‑ несмещенная оценка среднего квадратического отклонения величины в1;

tкр (a, g=n-2) находится по таблице t-распределения при заданном a и g=n-2

г) Определение интервальной оценки для при заданном х=х0