Сам индекс отражает обобщенную доходность по отношению к предыдущему дню. Однако доходность вложений за определенный период можно рассчитать с помощью несложной формулы:

,

где Y - доходность вложений в ГКО, % годовых; I0 - значение СОЛ-индекса на момент начала периода инвестиций; I1 - значение СОЛ-индекса на момент окончания периода инвестиций; t - продолжительность периода инвестиций, дней.

Говоря о недостатках подхода, отметим, что при моделировании возникает нелинейность (в веса входят цены облигаций, и, следовательно, в формулу они входят дважды). Если брать веса пропорционально количеству бумаг (т.е. использовать не реальные цены, а номиналы), то, на первый взгляд, проблема нелинейности устраняется. Однако приоритет был отдан соответствию формулы и выбранной экономической интерпретации.

Кстати говоря, даже если бы мы и взвешивали по количеству бумаг, нелинейность обеспечивалась хотя бы за счет того, что количество обращающихся на рынке выпусков меняется практически не реже одного раза в две недели, и вообще линейность фактически нарушалась бы при каждом аукционе/погашении/доразмещении. Первоначально мы специально рассчитали индекс в двух вариантах с различным подходом к взвешиванию и получили расхождение только в третьем знаке, причем на интервале более полугода. Решающим аргументом в пользу капитализационного (денежного) взвешивания стало то обстоятельство, что в этом случае динамика индекса не испытывает резких скачков при погашении/аукционе, так как деньги от погашения, как правило, перетекают на вторичные торги.

Приложение 2. SOBI-GKO-yield (обобщенный индекс ГКО). Методика расчета и рекомендации по использованию

1. Общая информация об индексе

SOBI-GKO-yield рассчитывается для ГКО с октября 1995 года по данным ММВБ.

Индекс регулярно публикуется в бюллетенях "Финансовый рынок", "Финансовый маркетинг", системах Reuters, Bloomberg.

2. Цель расчета

Определить общую тенденцию движения доходности рынка.

Для уровня доходности наиболее корректным индикатором, в широком смысле этого слова, является кривая распределения эффективных процентных ставок (yield curve). Она имеет явное преимущество перед точечными (агрегированными) показателями, поскольку, во-первых, позволяет оценить уровень ставок на конкретный срок и на конкретный отрезок времени, а во-вторых, снимает проблему корректного усреднения показателей доходности отдельных выпусков. Однако не всегда быстро удается определить, что же меняется - форма самой кривой или ее общий уровень. Точечный индикатор может помочь решить эту проблему.

3. Описание гипотез

· Любую ценную бумагу можно рассматривать как совокупность потоков платежей.

· Совокупность обращающихся на рынке дисконтных бумаг можно считать одной синтетической купонной облигацией.

· Все промежуточные выплаты будут реинвестированы под один и тот же процент.

4. Экономическая интерпретация

Действительно, если принять первую гипотезу, потоки платежей синтетической облигации эквивалентны совокупности потоков платежей всех обращающихся ГКО. Датой погашения этой облигации является дата погашения ГКО той серии, которая имеет наиболее длительный период до погашения в текущий момент. Синтетическая облигация погашается по номинальной стоимости этого выпуска, в качестве купонов выступают выплаты, осуществляемые при погашении остальных, более “коротких” ГКО.

5. Определение множества возможных математических моделей

Классическая формула, применяемая для расчета доходности купонной облигации, имеет следующий вид:

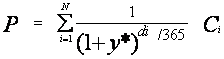, (1)

где Р — рыночная стоимость синтетической облигации (т.е. портфеля, состоящего из ГКО всех обращающихся выпусков); N — количество обращающихся выпусков ГКО; Ci — объем погашения i-го выпуска ГКО; у* — доходность к погашению синтетической облигации — обобщенная рыночная доходность (с учетом реинвестирования “купонов”); di — количество дней до погашения i-го выпуска ГКО.

Важно, чтобы в левой и правой частях формулы стояли величины одинаковой размерности. Фактически Ci представляет собой vi — объем в обращении i-й облигации (на конкретный день). Под рыночной ценой портфеля в левой части формулы в этом случае следует понимать сумму (vipi), где pi — средневзвешенная (за торговую сессию) цена соответствующей бумаги в виде доли от номинала (0,7; 0,8 и т.п.); vi — объем в обращении.

Уравнение (1) можно решить одним из итерационных методов. Найденная в результате обобщенная процентная ставка y* отражает доходность к погашению синтетической облигации.

Кроме того, для определения показателя обобщенной доходности можно пользоваться обобщенной ставкой duration weighted yield, которая является хорошим приближением решения уравнения (1). Таким образом, в качестве индикатора обобщенной доходности можно пользоваться следующим выражением:

, (2)

где — весовой объемный коэффициент каждого выпуска ГКО,

;

yi — эффективная доходность к погашению ГКО i-й серии;

—количество дней до погашения i-го выпуска ГКО;

— средний срок до погашения портфеля всех обращающихся облигаций.

После несложных преобразований формула (2) принимает следующий вид:

, (3)

6. Описание выбранной модели

Индекс расcчитывается путем численного решения уравнения (1) методом хорд. Выбор в пользу численного решения уравнения (1) по сравнению с приближенным аналитическим решением сделан в связи со следующими соображениями. Программные средства позволяют без особых затрат в быстрые сроки рассчитать точное решение уравнения с любой допустимой погрешностью. Следовательно, использовать хотя бы и аналитическое, но приближенное решение вряд ли целесообразно.

7. Учет технических моментов

Необходимости в подобном учете не возникло.

8. Достоинства и недостатки. Рекомендации по использованию

· Гипотеза о том, что все промежуточные выплаты будут реинвестированы под один и тот же процент, пока еще для российского рынка является слишком сильной. Данное допущение уместно для очень стабильной долгосрочной конъюнктуры процентных ставок.

· Метод расчета индекса путем численного решения некоторого уравнения затрудняет его расчет непрограммными средствами (вручную). Скорость расчета индекса становится критической в случае, если расчет необходимо производить очень часто и в очень сжатые сроки. Таким образом, человек, не имеющий возможности пользоваться хотя бы электронными таблицами, самостоятельно рассчитать индекс не сможет.