6.2. Создание и обоснование оптимальных параметров

уборочного модуля

Установлено [42, 71, 76, 77, 77, 78, 79, 82, 85, 90, 93, 99, 109, 111, 113, 116, 118, 125], что в модуле объективен стык формировок крон многолетних растений с нагрузкой урожаем по формам 1, 3, 4, 5 и 6 и урожая со средствами уборки по форме 4 (рис. 11). Стык элементов крон растений с нагрузкой урожаем исследовался в системе «Рокрас» [125], Краснодарском способе формирования виноградного куста [111] и способе ведения укрывной культуры винограда [113]. За критерий стыка положено свойство ускоренного роста и развития растений под влиянием создаваемого аллелопатического воздействия друг на друга корневых систем разной силы потенциального роста (по форме 4), страдальческого положения элементов кроны (по формам 1, 3, 5 и 6) и преимущественного соотношения корневой системы к надземной части. Так же - принцип структурного построения механизированных технологий на стыке системы машина - растение через внешние параметры крон с учётом целесообразного ветвления в каждом порядке (табл. 4).

Аллелопатическое воздействие исследовалосьв 1983 . 1993 годах в ОПХ «Азовское» НПО «Дон» в насаждении яблони с переменным размещением деревьев на подвоях с различным потенциальным ростом по «организму»

(табл. 1). Уходные работы проводились агрегатами сначала по четырёхметровому междурядью, а после удаления деревьев на подвое с меньшим потенциальным ростом - по шестиметровому. Критерием смены направления проходов служил предел деформации горизонтальной площади проекции кроны в параметрах её золотого сечения 0,74d : 1,2d (разд. 2). В конечном итоге экспериментальный сад вступил в пору плодоношения с третьего года посадки, а контроль - с четвёртого. В сумме за 7 лет плодоношения сад экспериментальный дал 577 ц/га яблок, а контроль - 333 ц/га.

В экспериментальном саду кроны деревьев формировались из плодовых плетей по варианту 1 в пределах иерархии рангов ветвления (табл. 4). В результате на третий год кроны имели не менее 12 плетей. Из - за малой толщины, нагружаясь урожаем, листьями и собственной массой по формам 1 и 3 (рис. 11) плети приобретали пониклую форму (страдальческую), что обеспечивало к моменту уборки урожая сдерживание высоты кроны. Уборка осуществлялась в первом ярусе без лестниц. То есть, получен исключительный конечный результат ИКР (Г.Альтшулер, 1973), когда действие выполняется без применения технических средств [93, 94, 125].

Страдальческое положение элементов кроны осуществлялось изучением физико - механических свойств порослевых и волчковых побегов на предмет их использования взамен отплодоносивших частей куста в Краснодарском способе формирования куста [111] и способа ведения укрывной культуры винограда [113]. Установлено, что каждый элемент этих формировок строит свои вегетирующие части на втором году жизни кордона согласно зависимости (21). Величина роста побегов и количественное распределение соцветий по этим побегам в интервале проекций элементов на погонный метр ряда может быть отображена непрерывной неотрицательной функцией , а насыщенность кордона по длине каждого элемента может быть определена, как площадь фигуры, ограниченной криволинейной трапецией с основанием или или (рис. 21)

Рис. 21. Распределение соцветий по длине элементов:

а) Краснодарского способа формирования куста;

б) способ ведения укрывной культуры винограда

Это аналогично задаче о работе переменной силы, где величина соцветий или величина роста побегов уподобляется силе (прошлогодний побег «работает», выдавая в виде продукта длину прироста побегов, или количество соцветий на нём). Так как плодоносящего прироста на побеге больше единицы и каждый из них «работает», то «работа» одного элемента определяется сложением «работ» каждого плодоносящего прироста изучаемого года

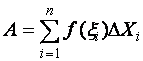, (47)

где - интервал между плодоносящими побегами.

Сумма (47) в данном случае зависит от способа разбиения проекции элемента на погонную длину ряда. В нашем случае шаг разбиения не может быть больше длины междоузлия, но может стремиться к нулю, если отрезок прошлогоднего побега поворачивать с горизонтального положения до вертикального, как это показано в форме 5 отрезком АВ или форме 6 отрезком АО (рис. 11).

Приняв во внимание тот факт, что шаг разбиения не может быть больше величины междоузлия, тогда выражение (47) запишется

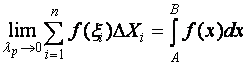, (48)

где - шаг разбиения отрезка [AB];

[AB] - промежуток интегрирования.

Но, по данным наших исследований , тогда выражение (48) запишется как площадь

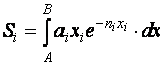, (49)

где - площадь криволинейной трапеции с основанием [AB], ограниченной сверху кривой .

Так как на одном основании [AB] (рис. 21) располагаются три площади криволинейных трапеций, каждая из которых сверху ограничена подобными кривыми типа , но с различными величинами и , а также с разным шагом разбиения , то в конечном итоге способы [111] и [113] могут быть формализованы одной математической моделью