ü Занятие №5

Цель. Познакомить детей с образованием числа 9 и упражнять их в счете в пределах 9; показать независимость числа предметов от площади, которую они занимают; закрепить умение устанавливать соотношения между предметами по высоте и толщине; раскладывать их в ряд в порядке убывания (возрастания) высоты или толщины; показать, что место, занимаемое предметом среди других, изменяется в зависимости от того, по какому признаку предметы сравниваются.

Что касается экспериментальной группы, то здесь занятия проводились по методике Т.А. Остапенко, основе которой лежит использование игровых приемов в процессе формирования элементарных математических представлений дошкольников группы «Почемучки». В данной группе было проведено 5 тематических занятий по следующим темам:

1. «Осень».

Программное содержание: закреплять знания детей об осени как времени года; учить цветовому обозначению времен года; знакомить с цифрой 5; формировать знания об образовании числа 5 из единиц; развивать умение ориентироваться на листе бумаги; закреплять знание цифры 4; закреплять счет до 5; закреплять знание геометрических фигур (круг, треугольник, квадрат); развивать память, внимание

2. «Грибы»

Программное содержание: закреплять знания детей о грибах, формировать знания об образовании числа 6 из единиц; знакомить с цифрой 6; обучать делению множества предметов пополам; закреплять знание геометрических фигур (круг, треугольник, квадрат, овал), цифр 1, 2, 3, 4, 5; закреплять умение считать до 6; развивать воображение, мышление, мимику.

3. «Овощи»

Программное содержание: закреплять знания детей об овощах; формировать умение ориентироваться по плану группы; правильно определять взаимное расположение предметов в пространстве; учить выполнять движения в определенном направлении, повторять цифры 1, 2, 3, 4, 5, 6; закреплять счет в пределах шести; учить составлять геометрические фигуры из палочек и ниток, обследовать их, анализировать; развивать память, мышление, воображение.

4. «Фрукты и ягоды»

Программное содержание: закреплять знания о фруктах и ягодах; знакомить с образованием числа 7; закреплять счет в пределах семи, цифры 1, 2, 3, 4, 5, 6; учить выделять из совокупности предметы, отличающиеся по какому-либо признаку; формировать умение объединять предметы со сходными признаками; формировать представление о ритме, учить самостоятельно составлять узор с ритмичным повторением элементов; развивать воображение, мышление.

5. «Дом, квартира»

Программное содержание: закреплять знания детей о различных видах домов у людей и животных; закреплять знания о геометрических фигурах (круг, овал, квадрат, треугольник); знакомим» с цифрой восемь; уточнять представление об объемных телах — кубе и пирамиде, закреплять умение соотносить цифры с количеством; закреплять порядковый счет в пределах девяти; учить строить сериационный ряд; учить находим, различия в похожих предметах; развивать память, внимание, воображение.

2.3 Результаты проведенного исследования

Проанализировав результаты диагностики математического развития детей среднего дошкольного возраста до начала исследования мы установили, что:

1. из 12 обследуемых детей среднего дошкольного возраста в контрольной группе на начало исследования были выявлены следующие уровни математического развития:

ü Оптимальный уровень – 2 ребенка – 16,7%

ü Достаточный уровень: ‒ 6 детей – 50%

ü Недостаточный уровень: ‒ 3 ребенка – 25%

ü Критический уровень: ‒ 1 ребенок – 8,3%

2. В экспериментальной группе на начало исследования были выявлены следующие уровни математического развития:

ü Оптимальный уровень: ‒ 2 ребенка – 16,7%

ü Достаточный уровень: ‒ 7 детей – 58,3%

ü Недостаточный уровень: ‒ 2 ребенка – 16,7%

ü Критический уровень: ‒ 1 ребенок – 8,3%

Предъявим данные в таблице (Таблица 2.2.1)

Таблица 2.2.1 – Результаты изучения уровней математического развития детей среднего дошкольного возраста на момент начала исследования

Для проведения сравнительного анализа результатов исходного уровня математического развития детей среднего дошкольного возраста контрольной и экспериментальной групп, отобразим данные в диаграмме (рисунок 2.2.1)

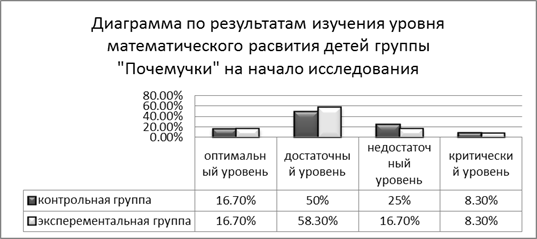
Рисунок 2.2.1

Как показывает диаграмма исходного уровня математического развития детей среднего дошкольного возраста контрольной и экспериментальной группы почти одинаковые, разница составляет 8,3% в достаточном и 4,3% в недостаточном уровнях.

С целью изучения проблемы использования игровых приёмов при формировании элементарных математических представлений у дошкольников, нами были проведены комплекс занятий по математике в контрольной группе по методике А.С. Метлиной и в экспериментальной – по методике Т.А. Остапенко.

После чего осуществили повторную диагностику математического развития детей среднего дошкольного возраста, где получили следующие данные:

1. В контрольной группе:

ü Оптимальный уровень – 2 ребенка – 16,7%

ü Достаточный уровень: ‒ 6 детей – 50%

ü Недостаточный уровень: ‒ 4 ребенка – 33,3%

ü Критический уровень: ‒ 0 ребенок – 0%

2. В экспериментальной группе:

ü Оптимальный уровень: ‒ 5 ребенка – 41,7%

ü Достаточный уровень: ‒ 7 детей – 58,3%

ü Недостаточный уровень: ‒ 0 ребенка – 0%

ü Критический уровень: ‒ 0 ребенок – 0%

Для проверки эффективности использования игровых приемов при формировании элементарных математических представлений у дошкольников и сопоставив уровни математического развития детей контрольной и экспериментальной групп, на момент проведения нашего исследования: мы определили, что в уровня математического развития детей экспериментальной группы произошли положительные изменения. В группе было выявлено 5 детей, у которых уровень математического развития оптимальный (41,7%), из них у двоих детей на начало исследования был достаточный уровень, а у одного недостаточный уровень сформированности элементарных математических представлений. Произошли количественные изменения в критическом уровне. Один ребенок с критическим уровнем математического развития поднялся до достаточного уровня.