Из специальной теории относительности следует, что длина тела и длительность происходящих в нем процессов являются не абсолютными, а относительными величийами. При приближении к скорости света все процессы в системе замедляются, продольные (вдоль движения) размеры тела сокращаются и события, одновременные для одного наблюдателя, оказываются разноименными для другого, движущегося относительно него.

Если принять предположение классической механики об абсолютном характере расстояний и времен, то уравнения преобразования пространственных координат и времени при

переходе от покоящейся системы отсчета к движущейся вдоль оси х относительно него равномерно прямолинейно со скоростью v системе отсчета будут иметь следующий вид:

Скромное равенство t1 = t означало, что во всех системах отсчета время течет одинаково, слова "сейчас", "настоящий момент" имеют абсолютный смысл (факт, представлявшийся очевидным до начала XX столетия). Эти уравнения часто называют преобразованиями Галилея. Если же преобразования должны удовлетворять также требованию постоянства скорости света, то они описываются уравнениями Лоренца, названными по имени нидерландского физика Хендрика Антона Лоренца, и имеют вид:

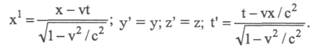
Теперь следует говорить не о системе координат, а о системе отсчета, т. е. о совокупности системы координат и часов. Абсолютности времени больше нет, каждая система отсчета характеризуется своим собственным временем. Указывая момент времени, надо указывать также соответствующую систему отсчета. Все это явно проявляется лишь при достаточно больших относительных скоростях систем; если же vс, то, как легко видеть, преобразования Лоренца переходят в преобразования Галилея — специальная теория относительности переходит в классическую механику как свой предельный случай.

Эйнштейн отмечает, что неподвижный наблюдатель воспринимает проносящееся мимо него шарообразное тело в виде сплюснутого эллипсоида вращения. С точки зрения наблюдателя, движущегося вместе с телом, оно, как и прежде, сохраняет форму шара, однако все предметы, не движущиеся вместе с этим наблюдателем, точно таким же образом представляются ему укороченными в направлении движения. Этот результат оказывается не таким уж странным, если учесть, что это высказывание о размерах движущегося тела имеет весьма сложный смысл, поскольку теперь размеры тела можно определить только с помощью измерения времени. Пространство и время рассматриваются теперь во взаимосвязи.

Опираясь на преобразования Лоренца, легко проверить, что движущаяся твердая линейка будет короче покоящейся, и тем короче, чем быстрее она движется:

Если принять скорость света бесконечно большой, то при постановке ее в уравнения Лоренца последние переходят в уравнения Галилея. Но специальная теория, как известно, постулирует постоянство скорости света. Этот постулат следует из уравнений электромагнитных процессов Максвелла. Чтобы согласоваться с постулатами специальной теории относительности, классическая механика нуждалась в некоторых изменениях. Например, если во втором законе Ньютона (F = та) масса считалась постоянной, в теории относительности она зависит от скорости движения и выражается формулой

Когда скорость тела приближается к скорости света, масса его неограниченно растет и в пределе приближается к бесконечности. Поэтому, согласно теории относительности, движения со скоростью, превышающей скорость света, невозможны. Движения со скоростями, сравнимыми со скоростью света, впервые удалось наблюдать на примере электронов, а затем и других элементарных частиц. Тщательно поставленные эксперименты с такими частицами действительно подтвердили предсказания теории об увеличении их массы с возрастанием скорости.

В 1905 г. А. Эйнштейн пришел к заключению, что масса тела есть мера содержащейся в нем энергии. Позднее он формулирует следующий важный вывод специальной теории относительности: масса и энергия эквивалентны друг другу — появляется знаменитая формула Эйнштейна, связывающая энергию и массу:

При достаточно больших скоростях (в этом случае говорят о релятивистской физике) специальная теория относительности приводит к общему выражению для энергии:

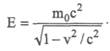
Через m0 обозначена масса покоя (масса тела в системе отсчета, связанной с этим телом), а Е — энергия тела, рассматриваемая в системе, относительно которой тело движется со скоростью v.

До создания специальной теории относительности законы сохранения энергии и массы рассматривались как два самостоятельных закона сохранения. Теперь же оба этих закона слились в один. По выражению Эйнштейна, масса должна рассматриваться как "сосредоточие колоссального количества энергии".

Таким образом, влияние специальной теории относительности выходит далеко за пределы тех проблем, из которых она возникла. Она снимает трудности и противоречия теории поля; она формирует более общие механические законы; она заменяет два закона сохранения одним; она изменяет наше классическое понятие абсолютного времени. Ее ценность не ограничивается лишь сферой физики; она образует общий остов, охватывающий все явления природы.

Однако экспериментальные данные о постоянстве скорости света и вытекающие из этого относительность времени и пространства приводят к парадоксам, для разрешения которых понадобилось введение принципиально новых представлений. Например, одним из таких парадоксов является парадокс близнецов.

Парадокс близнецов. Поскольку в равномерно движущемся с огромной скоростью космическом корабле темп времени замедляется и все процессы происходят медленнее, чем на Земле, то космонавт, вернувшись на нее, окажется моложе своего брата-близнеца.

Рассмотрим двух близнецов А и В в возрасте 20 лет. Один из них (В) отправляется в космическое путешествие к звезде Арктур на корабле, летящем со скоростью 0,99 с. Для жителей Земли расстояние до звезды Арктур составляет 40 световых лет. Сколько лет будет близнецам А и В, когда В, закончив свое путешествие, вернется обратно на Землю?

С точки зрения близнеца А, путешествие, чтобы долететь до звезды и обратно, займет 80 лет, т. е. когда В вернется, возраст А будет 20 + 80= 100 лет.

С точки зрения близнеца В, часы на космическом корабле будут идти медленнее враза. Это значит, что за время путешествия на корабле пройдет 80 лет, умноженные на 0,141, или 11,4 года. Итак, к концу путешествия близнец В будет в возрасте 20 + 11,4 = 31,4 года. Следовательно, он окажется моложе своего брата, оставшегося на Земле, на 68,6 года. Космический путешественник не чувствует, что его время идет медленнее. В приведенном примере расстояние до звезды Арктур кажется близнецу В укороченным благодаря лоренцевому сокращению. По его измерениям расстояние от Земли до звезды Арктур составляетсветовых лет, или5,64 световых лет, а чтобы долететь до Арктура и вернуться обратно — 11,4 года. Этот результат согласуется с вычислениями близнеца А, оставшегося на Земле.