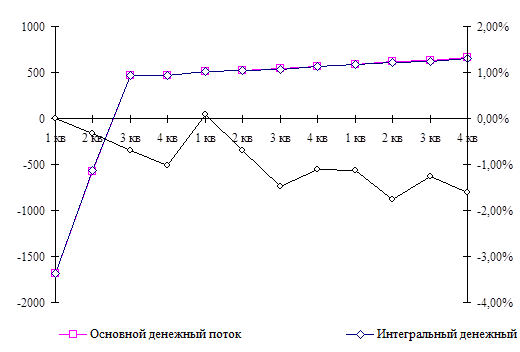
Рисунок 8. График основного и интегрального денежных потоков

Таблица 11.

Сводная таблица основного и интегрального денежного потока (полученного по методу Монте-Карло)

Теперь рассчитаем дисперсию денежного потока и на ее основе определим дисперсионное отклонение по денежному потоку. Согласно рассмотренной выше методологии и правилам статистического расчета по анализу рядов динамики дисперсия определяется по формуле:

(27)

где – интегральное значение денежного потока;

Теперь оценим дисперсию для каждого отдельного периода инвестиционного проекта и представим их в виде таблице (см. Приложение 4).

Несомненно, предлагаемая мной выборка относительно мала, и позволяет с достаточно большой долей вероятности спрогнозировать конечную оценку инвестиционного проекта.

На основании анализа дисперсии, что средние отклонение по величине дисперсии составляет 5,76%. На основании показателя дисперсии можно сделать вывод, что при 20% (±5% по каждой составляющей денежного потока) при выборке в 100 отклонений средние дисперсионное отклонение составит 5,76%. Это означает, что с точностью ±10% мы имеем право утверждать, что оценка предлагаемого инвестиционного проекта будет равна 3277±188,8 тыс.руб.

3.4 Сравнение результатов по методам оценки инвестиционных проектов

Теперь необходимо сравнить полученные результаты.

На основании произведенных расчетов сравним денежные потоки, полученные методами дисконтирования, анализа чувствительности и методом «Монте-Карло». При этом денежного потока полученного при оценке инвестиционного проекта на чувствительность, берется денежный поток с учетом инфляции по варианту с нулевым отклонением. Результаты можно представить в таблице (см. табл.12). Представим полученные результаты на графиках, для денежных потоков и накопленных денежных потоков (см. рис.9).

Таблица 12.

Результаты расчета денежных потоков по трем методам оценки