Содержание:

Введение . 3

1. Вывод уравнения, описывающего высокочастотные резонансные колебания давления неоднородного газа в трубе 5

2. Определение собственных чисел и собственных функций методом Ритца. 12

3. Анализ результатов 25

Выводы . 27

Литература . 28

Приложение 1 29

Приложение 2 42

Введение.

В различных газо-технических агрегатах часто возникают сильные нелинейные колебания. Обычно возникновение таких колебаний нежелательно, поскольку они нарушают расчетный режим работы агрегата и даже могут привести к выходу его из строя.

Так одной из важных задач в компрессоростроении является борьба колебаний межступенчатых коммуникаций аппаратов. Причиной являются возмущающие силы, вызванные большой амплитудой колебаний газа в коммуникациях. Колебания газа, воздействуя на компрессор, могут изменить его производительность и вызвать перерасход энергии.

Нелинейные колебания легко возникают в ЖРД. Колебания увеличивают местные коэффициенты теплоотдачи, механические и тепловые напряжения, что может привести к разрушению элементов конструкций. Подобные явления могут возникать также в газотурбинных установках, мощных парогенераторах, в тепловых контурах АЭС и т.д.

С другой стороны, нелинейные колебания могут существенно интенсифицировать горение, повышать теплонапряженность топочных камер, улучшать тепло и массообмен, снижать гидравлическое сопротивление. В настоящее время генераторы нелинейных колебаний нашли применение при очистке поверхности нагрева котлоагрегатов, а также при распылении жидкости в промышленной экологии.

Одно из перспективных направлений развития техники – это разработка волновых газовых холодильных машин, в которых реализуются резонансные режимы колебаний газа. Достижение низких температур при помощи таких установок открыло бы принципиально новые возможности при решении многих задач физики, электроники, энергетики систем связи, вычислительной техники, биологии, медицины и др.

В сложных системах, таких как трубопроводы или камеры внутреннего сгорания, колебания генерируются сочетанием более простых источников возбуждения, как поршень, периодический тепло- или массопровод, набегающая в трубу струя. Кроме того, между колебаниями параметров газа и тепло- массопроводом может возникать обратная связь, тогда колебания могут становиться самовозбуждающимися. Теория нелинейных колебаний, когда они возбуждаются сочетанием нескольких источников остается пока не разработанной. Поэтому актуальной является разработка методики исследований резонансных колебаний, возникающих в более простых установках, в частности, в трубе, на одном конце которой находится гармонически колеблющийся поршень. Другой конец трубы может быть закрыт (закрытая труба) или сообщаться с окружающей средой (труба с отрытым концом). Труба может быть заполнена однородным газом, например, воздухом или другим газом при постоянной температуре. Если средняя температура изменяется по длине трубы, то меняются и другие физические свойства. Это случай колебаний неоднородного газа. Наиболее исследованы резонансные колебания в трубе с поршнем и заполненным однородным газом. Задачи определения резонансных частот и амплитуды колебаний давления в этом случае облегчается тем, что она сводится к решению уравнения

, (1)

где p –амплитуда колебаний давления, x –осевая (вдоль оси трубы), k2 –комплексная константа при соответствующих граничных условиях на концах. Как известно, уравнению удовлетворяют две собственные функции sinkx, coskx. Cобственные числа определяются из граничного условия на x=L, где L –длина трубы.

В настоящей работе поставлены задачи:

а) вывести уравнение, описывающее высокочастотные резонансные колебания давления неоднородного газа в трубе,

в) выполнить приближенный расчет собственных чисел и собственных функций этого уравнения в случае неравномерного распределения температуры.

1. Вывод уравнения, описывающего высокочастотные резонансные колебания давления неоднородного газа в трубе.

Рассмотрим колебания в длинной цилиндрической трубе (L<<R, L-длина, R-радиус трубы), заполненной газом. Примем H>>1 (случай высокочастотных колебаний). Волновое уравнение в первом приближении, учитывающее пристеночное поглощение, а также наличие осевого градиента температуры и форму канала, получено Роттом:

, (2)

где

J0,J1-функции Бесселя нулевого и первого порядка, p-колебания давления, a-скорость звука, Тm-средняя по времени температура газа в трубе, ω-циклическая частота, σ-число Прандтля.

При R=const. И N=1 (теплоемкость стенки трубы выше теплоемкости газа) уравнение (2) выглядит следующим образом:

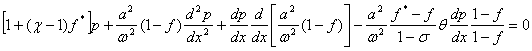(3)

Уравнение (3) можно переписать в виде:

где

, (4)

Последнее слагаемое уравнения есть производная от произведения, следовательно, можно переписать его в виде:

Здесь сумма двух последних слагаемых также есть производная от произведения, поэтому запишем уравнение следующим образом:

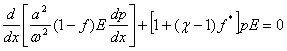(5)

Пусть

(6)

Перепишем (5) с учетом H*:

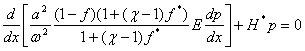(7)

Так как

,

уравнение (7) примет вид:

(8)

Упростим это уравнение, оценив величину E. Пусть средняя температура изменяется по закону (распределение средней температуры по длине трубы показано на рис.1):

(9),

где

, (10)

T1-температура в начале трубы,

Т2-температура в конце трубы.

Запишем скорость звука:

, (11)

Вычислим величину θ, входящую в (4):

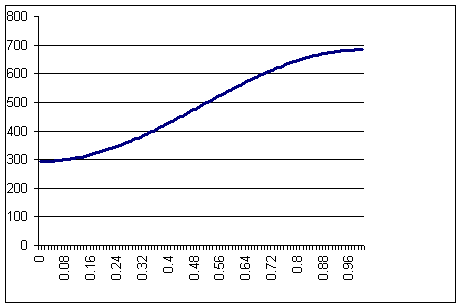
Рис.1: Распределениесредней температуры вдоль оси трубы при e = 0.4. Т1 = 293К

На рис.1 показано распределение средней температуры вдоль оси трубы для έ = 0.4, Т1 = 293К. В зависимости от έ крутизна графика изменяется.

(12)

Рассмотрим уравнение (5) при высокочастотных колебаниях. Тогда величины f, f* будут иметь вид: