s0 £ s, S £ S0.

Иначе говоря, от добавления новых точек деления нижняя сумма не уменьшается, а верхняя не увеличивается.

Доказательство. Допустим, что

yi < < yi+1. (3)

Тогда при k ¹ i полусегменты [yk, уk+1), а с ними и множества ek, фигурируют и в новом способе дробления. Полусегмент же [yi, yi+1) при переходе к новому способу заменяется двумя полусегментами

[yi,), [, yi+1),

в связи с чем и множество ei разбивается на два множества

= E(yi £ f < ), = E(£ f < yi+1).

Очевидно, что

ei = +, = 0,

так что

mei = m + m. (4)

Из сказанного ясно, что сумма s получается из суммы s0 заменой слагаемого yimei двумя слагаемыми yim + m, откуда, в связи с (3) и с (4), и следует, что s ³ s0.

Для верхних сумм рассуждение аналогично.

Следствие. Ни одна нижняя сумма s не больше ни одной верхней суммы S.

Доказательство. Рассмотрим два каких-нибудь способа дробления I и II, сегмента [А, В]. Пусть этим способам отвечают соответственно нижние суммы s1 и s2 и верхние суммы S1 и S2.

Составим третий способ дробления [А, В] - способ III, в котором точками деления служат точки деления обоих способов I и II. Если способу III отвечают суммы s3 и S3, то, в силу леммы, s1 £ s3, S3 £ S2, откуда, в связи с тем, что s3 £ S3, ясно, что s1 £ S2, а это и тре­бовалось доказать.

Выберем какую-нибудь определенную верхнюю сумму S0. Так как для всякой нижней суммы s будет s £ S0, то множество {s} всех нижних сумм Лебега оказывается ограниченный сверху. Пусть U есть его точная верхняя граница U = sup{s}.

Тогда, ясно, что

U £ S0.

Ввиду произвольности суммы S0, последнее неравенство доказы­вает, что множество {S} всех верхних сумм Лебега ограничено снизу. Назовем через V его точную нижнюю границу

V = inf{S}.

Очевидно, при любом способе дробления будет

S £ U £ V £ S.

Но, как мы отмечали, S – s £ lmE, откуда

0 £ V – U £ lmE

и, так как l произвольно мало, то

U = V.

Определение. Общее значение чисел U и V называется инте­гралом Лебега функции f(x) по множеству Е и обозначается символом

(L)

В тех случаях, когда смешение с другими видами интеграла исключено, пишут просто

В частности, если Е есть сегмент [а, b], употребляют символы

(L)

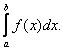
Из сказанного выше следует, что каждая измеримая ограни­ченная функция интегрируема в смысле Лебега, или, короче, инте­грируема (L). Уже из этого замечания видно, что процесс интегри­рования (L) приложим к гораздо более широкому классу функций, чем процесс интегрирования (R). В частности, совершенно отпадают все вопросы, связанные с признаками интегрируемости, которые для интегралов (R) имеют сравнительно сложный характер.

Теорема 1. Если l ® 0, то суммы Лебега s и S стремятся

к интегралу

Теорема непосредственно вытекает из неравенств

S £ £ S, S – s £ l× mE.

Из этой теоремы, между прочим, следует, что значение инте­грала Лебега, которое в силу самого определения его связано с числами А и В, на самом деле от них не зависит.

Действительно, допустим, что

A < f(x) < В, A < f(x) <B*,

причем В* < В. Раздробим сегмент [А, В] на части

A = у0 < у1 < ¼ < yn = В,

причем включим и точку В* в число точек деления В* = ут.

Если мы составим множества ek, то легко убедиться, что

ek = 0 (k ³ m).

Значит,

s = = = s*,

где s* есть нижняя сумма Лебега, построенная, исходя из сег­мента [А, В*]. Сгущая точки дробления и переходя к пределу, най­дем, что

I = I*,

где I и I* суть значения интегралов Лебега, отвечающие сегмен­там [А, В] и [А, В*]. Таким образом, изменение числа В не отра­жается на величине интеграла. То же относится и к числу А. Этот факт весьма существенен, ибо только теперь определение интеграла оказывается освобожденным от случайного характера выбора то­чек А и В.

3. Основные свойства интеграла

В этом параграфе мы установим ряд свойств интеграла от огра­ниченной измеримой функции.

Теорема 1. Если измеримая функция f(x) на измеримом мно­жестве Е удовлетворяет неравенствам a £ f(x) £ b, то

a× mE £ £ b× mE.

Это теорема обычно называется теоремой о среднем.

Доказательство. Пусть n натуральное число. Если мы положим

A = a - , B = b + ,

то окажется, что

A < f(x) < B,

и суммы Лебега можно будет составлять, дробя сегмент [А, В].

Но еслиA £ yk £ B, то, очевидно,

A£ £ B

или, что то же самое,

A× mE £ s £ B× mE,

откуда и в пределе

mE £ £ mE.

В силу произвольности числа n, теорема доказана.

Из этой теоремы вытекает несколько простых следствий.