1.2. Критерий качества (минимизируемый функционал)

Управление системой (3.1) осуществляется для достижения некоторых целей, которые формально записываются в терминах минимизации по u функ­ционалов J, определяемых управлением u и траек­торией х, где

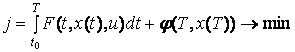(3.3)

Здесь F и заданные скалярные функции. Задача (3.1). (3.3) именуется задачей О.Больца; если , то задачей А.Майера и, наконец, задачей Лагранжа при .

1.3. Ограничения на траекторию

В некоторых реальных ситуациях траектория си­стемы не может принадлежать тем или иным частям пространства . Указанное обстоятельство находит отражение в ограничении вида ), где G(t) -заданная область в . В зависимости от конкретно­го типа этих ограничений выделяют различные классы задач управления. В задачах с фиксирован­ными концами начальное состояние и конеч­ное состояние х(Т) заданы. Если же x(t0) (или х(Т)) не задано, то получаем задачу со свободным левым (правым) концом. Задача с подвижными концами - это задача, в которой моменты t0 и T фиксированы, а векторы х(t0) и х(Т) принадлежат соответственно областям G(t0) и G(T). В ряде случаев ограничения носят интегральный характер и имеют вид

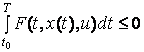
Если в задаче (3.1), (3.3) начальное положение x(t0) и конечное х(Т) заданы, моменты начала движения t0 и окончания T свободны, функция и , то получаем задачу о переводе системы (3.1) из положе­ния x(t0) в положение х(Т) за минимально возмож­ное время. Подобного рода задачи именуются зада­чами оптимальными по быстродействию.

1.4. Ограничения на управление

Информационные ограничения на управление зависят от того, какая именно информация о систе­ме (3.1) доступна при выработке управляющего воз­действия. Если вектор x(t) недоступен измерению, то оптимальное управление ищется в классе функ­ций u(t), зависящих только от t. В этом случае опти­мальное управление именуется программным. Если же вектор х(t) известен точно при , то опти­мальное управление ищется в классе функционалов и называется синтезом оптимального управ­ления (или управлением по принципу обратной связи). Здесь означает всю траекторию движе­ния на отрезке . Отметим, что принцип об­ратной связи является одним из центральных прин­ципов кибернетики. Техническим примером реализации принципа обратной связи являются центробежные регуляторы И.И. Ползунова (1766) и Дж. Уатта (1784), авиационный автопилот Д. Оль­ховского (1912) и братьев Сперри (1914), гидравли­ческий усилитель Л. Фарко (1873).

Кроме информационных ограничений возмо­жен и другой тип ограничений, обусловленный ог­раниченностью ресурсов управления, имеющих вид , где - заданное множество.

Подчеркнем, что для детерминированных задач (то есть задач, в которых уравнения движения, кри­терий качества и ограничения известны точно) опти­мальное значение критерия качества (3.3), реализуе­мое в классе программных управлений и управлений по принципу обратной связи, одно и то же.

2. УСЛОВИЯ ОПТИМАЛЬНОСТИ

2.1. Принцип максимума

Принцип максимума соответствует принципу Вейерштрасса и методу канонических уравнений Гамильтона в классическом вариационном исчис­лении. Сформулируем необходимые условия опти­мальности в форме принципа максимума для задач Майера

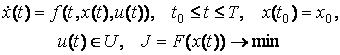(3.4)

Здесь - заданное множество, х0 - заданное начальное положение системы. Введем в рассмот­рение скалярную функцию Н и вектор сопряжен­ных переменных с помощью соотношений

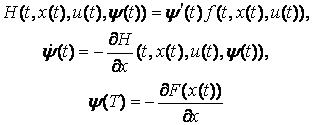(3.5)

где штрих - знак транспонирования.

Предположим, что u(t) - оптиматьное управле­ние, а х(t) и - соответствующие траектория и вектор сопряженных переменных, удовлетворяющие уравнениям (3.4), (3.5). Тогда функция достигает своего максимума по точке u(t)

(3.6)

Найдем из соотношения (3.6) зависимость u от то есть то есть

(3.7)

Далее подставим (3.7) в (3.4), (3.5). В результате получим краевую задачу для системы обыкновенных диффе­ренциальных уравнений относительно функций x(t) и , среди решений которой только и может находиться оптимальная траектория. Если опти­мальная траектория x(t) и вектор найдены, то оптимальное управление дается выражением (3.7). Отметим, однако, что поскольку соотношения (3.4) - (3.6) суть лишь необходимые условия оптимальности, то необходимо дополнительное обоснование опти­мальности траектории и управления, найденных из соотношений (3.4)-(3.6).

2.2. Метод динамического программирования

Метод динамического программирования явля­ется аналогом метода Гамильтона-Якоби, в кото­ром изучается все поле оптимальных траекторий. Опишем применение метода динамического про­граммирования для задачи (3.4). Выберем и зафикси­руем произвольный момент времени и рассмотрим вспомогательную задачу управления (3.4) на отрезке [t, T]. Обозначим через мини­мальное значение критерия качества во вспомога­тельной задаче при начальном условии , где х - произвольный вектор из . При некоторых предположениях функция V(t, x) удовлетворяет со­отношениям