В качестве примера можно снова рассмотреть открытый круг

Đ: Х12 + Х22 < 1.

Предположим, что Λс – критическая решётка области Đ. Ниже будет дан набросок доказательства того, что если критическая решётка существует, то она должна иметь три пары точек ±(А1, А2), ±(В1, В2), ±(С1, С2) на границе Х12 + Х22 = 1 круга Đ.

Если Λс не имеет точек на окружности Х12 + Х22 = 1, то можно будет получить Đ-допустимую решетку с меньшим определителем, гомотетически сжимая решетку Λс к началу координат, то есть рассматривая решетку L = tΛс точек (tX1, tX2), где (Х1, Х2) Î Λс , а t — это фикси­рованное число с условием 0 < t < 1. Тогда d(L) = t2d(Lc) < d(Lc) и, очевидно, L будет Đ-допустимой решеткой, если t достаточно близко к 1. Таким образом, решетка Lc содержит пару точек на окружности Х12 + Х22 = 1, координаты которых после надлежащего поворота осей мы можем считать равными ± (1, 0).

Если бы на окружности Х12 + Х22 = 1 не было бы больше точек решетки Lc, то мы смогли бы получить Đ-допустимую решетку L с меньшим определителем, сжимая решетку Lc в направлении, пер­пендикулярном оси X1, то есть принимая за L решетку точек (Х1, tХ2), где (Х1, Х2) Î Λс, а t достаточно близко к 1.

Наконец, если бы Λс имела бы только две пары точек ±(1, 0), ± (В1, В2) на границе, то решетку можно было бы слегка деформиро­вать так, чтобы точка (1, 0) осталась на месте, а точка с координатами (В1, В2) продви­нулась бы вдоль окружности Х12 + Х22 = 1 ближе к оси Х1. Наглядно это представлено на рисунке:

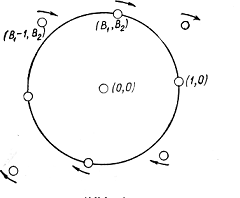
Данная операция, как легко проверить, уменьшает определитель, и при небольших деформациях получающаяся решётка Λ остаётся Đ-допустимой. Действительно, (1,0) и (В1, В2) можно рассматривать как базис решётки Λс, так как треугольник с вершинами (0, 0), (1, 0), (В1, В2), а следовательно, и параллелограмм, отвечающий базису (1, 0), (В1, В2) не содержит внутри себя точек Λс. Тогда критическая решётка Λс (если она существует) должна иметь три пары точек на окружности Х12 + Х22 = 1. Легко увидеть, что единственной решеткой, у которой три пары точек лежат на окружности Х12 + Х22 = 1, а одна из пар есть пара ± (1, 0), является решетка Λ ́ с базисом

(1, 0), (1/2, √3/4).

Она содержит вершины правильного шестиугольника

± (1, 0), ± (1/2, √3/4), ±(-1/2, √3/4),

лежащие на окружности Х12 + Х22 = 1, но не содержит ни одной точки (кроме (0, 0)) в круге Х12 + Х22 < 1. Таким образом, мы по­казали, что если Đ имеет критическую решетку, то Δ(Đ) = d(Λ ́) = (3/4)1/2. Минковский показал, что критические решетки существуют для довольно широкого класса областей Â, показав, грубо говоря, что любую Â-допустимую решетку Λ можно постепенно деформи­ровать до тех пор, пока она не станет критической.

“Неоднородная задача”

Другим общим типом проблемы является следующая типичная «неоднородная задача». Пусть f(х1,…,xn) — некоторая вещественнозначная функция вещественных аргументов х1, . . ., хn. Требуется подобрать постоянное число k со следующим свойством: если ξ1, ., ξn — любые вещественные числа, то найдутся такие целые числа u1,…,un, что

│f(ξ1 – u1,…, ξn – un)│≤ k.

Подобные вопросы естественно возникают, например, в теории алгебраических чисел. И на этот раз имеется простая геометрическая интерпретация. Для наглядности положим n = 2. Пусть Â — мно­жество таких точек (х1, х2) двумерной евклидовой плоскости, что

│f(x1, …, xn)│≤ k.

Пусть u1, u2 — любые целые числа; обозначим через Â(u1, u2) об­ласть, полученную из Â параллельным переносом на вектор (u1, u2); иными словами, Â(u1, u2) есть множество таких точек х1, х2, что

│f(х1 – u1, х2 – u2)│≤ k.

Неоднородная проблема состоит в выборе k таким образом, чтобы области Â(u1, u2) покрывали всю плоскость. Желательно выбрать k, а значит и Â, наименьшим из всех возможных (но так, чтобы свой­ство покрывать всю плоскость сохранилось). Здесь мы имеем про­тивоположность постановке однородной задачи, приведённой выше, где цель состояла в том, чтобы сделать области наибольшими, но все еще не пересекающимися одна с другой.

Список литературы.

1. Касселс, Дж. В. С. Геометрия чисел – М., Мир, 1965г.

2. Минковский Г. Геометрия чисел – Лейпциг, 1911г. (переиздание 1996г.)

3. Марков А. А. О бинарных квадратичных формах положительного определителя – СПб., 1948г.

4. Чеботарёв М. Г. Заметки по алгебре и теории чисел – УЧ Зап. Каз. Унив-та, 1934г. (переиздание 1994г.)

5. Чеботарёв М. Г. Доказательство теоремы Минковского о неоднородных линейных формах – М., Мир, 1949г.