БИЛЕТ 6 Отрезки параллельных прямых, заключенные м/у параллельными плоскостями, равны.

Для док-ва рассмотрим отрезки АВ и СD двух параллельных прямых, заключенные м/у параллельными плоскостями a и b. Докажем, АВ=СD. Плоскость j, проходящая ч/з параллельные прямые АВ и СD, пересекается с плоскостями a и b по параллельным прямым АС и ВD. Таким образом, в четырехугольнике ABDC противолеж. стор. паралл., т.е. ABDC-параллел-м

Но в пар-ме прот. леж. стороны равны, значит AB=CD.

Sп.п.=2pR(H+R)  

БИЛЕТ 5 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Для док-ва данного св-ва рассмотрим прямые а и b , по которым параллельные плоскости a и b пересекаются с плоскостью j. Докажем, что а| | b.

Эти прямые лежат в одной плоскости (j) и не пересекаются. В самом деле, если бы прямые а и b пересекались, то пл. a и b имели бы общ. точку, что невозможно, т.к. a| | b. Итак, прямые а и b лежат в одной плоскости и не пересекаются, а| | b.

2. Vпирамиды= 1/3*Sосн.*H  

БИЛЕТ 4 ОПРЕДЕЛЕНИЕ. Две плоскости называются параллельными, если они не пересекаются.

ТЕОРЕМА. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Док-во: Рассмотрим

две плоскости a и b. В

плоскости a лежат

пересекающиеся в т.М

прямые a и b, а в b -

- прямые а1 и b1,

причем а| | а1 и b| | b1.

Докажем, что плоскос.

-ти a и b не параллель

ны. Тогда они перес.

по прямой с. Мы получили, что плоскость a проходит ч/з прямую а, параллельную плоскости b, и пересекает плоскость b по прямой с. Отсюда следует, что

а| | с.

Но плоскость a проходит также ч/з прямую b, параллельную плоскости b. Поэтому b | | с. Таким обр. ч/з т.М проходят две прямые а и b, | | с. Но это невозможно, т.к. по теореме о параллельных прямых ч/з т. М проходит только одна прямая | | с.

Значит, наше допущение неверно и a| | b. Ч.Т.Д.

- - - - - - - -  

БИЛЕТ 3 ОПРЕДЕЛЕНИЕ. Прямая и плоскость

называются параллельными, если они не имеют общих точек.

ТЕОРЕМА. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Док-во: Пусть a-плоскость,

а - не лежащая в ней прямая

и а1 - прямая в плоскости a,

параллельная прямой а.

Проведем плоскость a1 ч/з

прямые а и а1.

Она отлична от a,

т.к. прямая а не ле-

жит в плоскости a. Плоскости a и a1 пересекаются по прямой а1. Если бы прямая а пересекала плоскость a, то точка пересечения принадлежала бы прямой а1. Но это невозможно, т.к. прямые а и а1 параллель-

ны. Итак, прямая а не пересекает плоскость a, а значит, параллельна плоскости a. Ч.Т.Д.

2. Vпараллелепипеда= Sосн.*H  

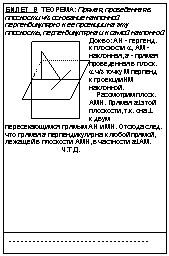
БИЛЕТ 2 ОПРЕДЕЛЕНИЕ. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

ТЕОРЕМА. Через точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Док-во: проведем ч/з а и

М плоскость a, а ч/з М в

в плоскости a прямую

b| | a. Докажем, что b| | a

единственна.

Допустим, что существует другая прямая b2| | a, и

проходящая ч/з т.М. Через b2 и а можно провести

плоскость a2, которая проходит ч/з М и а, след-но,

по Т.14.1(ЧЕРЕЗ ПРЯМ. И ТОЧКУ НЕ ЛЕЖ. НА

ЭТОЙ ПРЯМОЙ МОЖНО ПРОВЕСТИ ПЛОСКОСТЬ И ПРИТОМ ТОЛЬКО ОДНУ) она

совпадает с a. По аксиоме о параллельных

прямых b2 и а совпадают. Ч.Т.Д.

2. Vус.кон.=1/3*pH(R12+R1R2+R22)  

БИЛЕТ 1 А1 Какова бы ни была плоскость, существуют точки принадлежащие этой плоскости

и точки, не принадлежащие ей.

А2 Если две различные плоскости имеют общую

точку, то они пересекаются по прямой.

А3 Если две различные прямые имеют общую

точку, то ч/з них можно провести плоскость, и

притом только одну.

2. Sп.п.=Sбок.+Sосн.; Sбок.=Pосн.*A