Под информационными элементами понимают различные типы входных - N1, промежуточных - N2 и выходных - N3 данных, которые составляют наборы входных, промежуточных и выходных элементов данных.

Формализовано связи (парные отношения) между наборами информационных элементов отображаются в виде матрицы смежности В, квадратной бинарной матрицы, проиндексированной по обеим осям множеством информационных элементов D = {d1, d2, .,ds}, где s — число этих элементов:

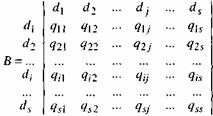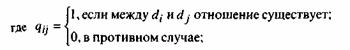В позиции (i,j ) матрицы смежности записывают 1 (т.е. qi j = 1), если между информационными элементами di и dj существует отношение rо, такое, что для получения значения информационного элемента dj необходимо непосредственное обращение к элементу di .

Наличие отношения между di и dj обозначают в виде, di rо dj т.е. q i j =1 ,

а отсутствие отношения — в виде di dj

Для простоты принимают, что каждый информационный элемент недостижим из самого себя: di = di ; i=

Матрице В ставится в соответствие информационный граф G = (D,rо). Множеством вершин графа G = (D,rо) является

множество D информационных элементов,

а каждая дуга di,dj соответствует условию di rо dj, т.е. записи 1 в позиции (i,j ) матрицы смежности В.

Например, задано множество D из четырех наборов информационных элементов, т.е. D = { d1, d2, d3, d4 }. Пусть матрица смежности В этих элементов имеет вид:

матрица смежности В Информационный граф

для этого примера G = (D,Ro) для этого примера

Из этой матрицы видно, что для вычисления элемента

d3 необходимо обращение к элементам d1 и d2, d4 — к элементу d3. Чтобы получить элемент d1, надо обратиться к d3- Элемент d2 не зависит от других элементов матрицы.

В общем случае, структура графа G = (D,R0) сложна для восприятия и анализа. Составленная на основе инфологической модели структура графа, не гарантирована от неточностей, ошибок, избыточности.

Для формального выделения входных, промежуточных и выходных наборов информационных элементов, определения последовательности операций их обработки, анализа и уточнения взаимосвязей на основе графа G = (D,Ro) строят матрицу достижимости.

Чем отличаются матрицы достижимости и смежности?

Для анализа информационных потоков в управляемой системе исходными являются данные о парных взаимосвязях, или отношениях (т.е. есть отношение или нет отношения), между наборами информационных элементов.

Под информационными элементами понимают различные типы входных - N1, промежуточных - N2 и выходных - N3 данных, которые составляют наборы входных, промежуточных и выходных элементов данных.

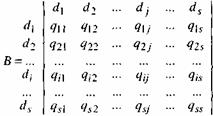Формализовано связи (парные отношения) между наборами информационных элементов отображаются в виде матрицы смежности В, квадратной бинарной матрицы, проиндексированной по обеим осям множеством информационных элементов D = {d1, d2, .,ds}, где s — число этих элементов:

В позиции (i,j ) матрицы смежности записывают 1 (т.е. qi j = 1), если между информационными элементами di и dj существует отношение rо, такое, что для получения значения информационного элемента dj необходимо непосредственное обращение к элементу di .

Наличие отношения между di и dj обозначают в виде, di rо dj т.е. q i j =1 ,

а отсутствие отношения — в виде di dj

Для простоты принимают, что каждый информационный элемент недостижим из самого себя: di = di ; i=

Матрицей достижимости М называют квадратную бинарную матрицу, проиндексированную по обеим осям множеством информационных элементов D аналогично матрице смежности В. Запись 1 в каждой позиции (i,j ) матрицы достижимости соответствует наличию для упорядоченной пары информационных элементов (di, dj) смыслового отношения достижимости R. Элемент dj достижим из элемента di , т.е.

выполняется условие di rо dj, если на графе G = (D,Ro) существует направленный путь от вершины di к вершине dj ( в процессе получения значения элемента dj используется значение элемента di ).

Если di dj , то отношение достижимости между элементами di и dj отсутствует и в позиции (i,j ) матрицы М записывают 0.

Записи 1 в j -м столбце матрицы М соответствуют информационным элементам di , которые необходимы для получения значений элементов dj и образуют множество элементов предшествования A(di ) для этого элемента. Записи 1 в i-й строке матрицы М соответствуют всем элементам dj , достижимым из рассматриваемого элемента di и образующим множество достижимости rоdj этого элемента.

Информационные элементы, строки которых в матрице М не содержат единиц (нулевые строки), являются выходными информационными элементами, а информационные элементы, соответствующие нулевым столбцам матрицы М, являются входными. Это условие может служить проверкой правильности заполнения матриц В и М, если наборы входных и выходных информационных элементов известны. Информационные элементы, не имеющие нулевой строки или столбца, являются промежуточными.

Для рассматриваемого примера матрицы В и М выглядят так:

Отличие столбцов матриц М и В объясняется тем, что в матрице М учитывается смысловое отношение R между информационными элементами, а в матрице В — только непосредственно rо. Например, элемент d4 в матрице М достижим из элементов d1, d2 и d3 т.е. d1 r d4, d2 r d4 и d3 r d4 , в то время как в матрице В для этих элементов d4 достижим только из d3, т.е. только d3 r0 d4.