где ΔТ — средний темп прироста;

Т — средний темп роста.

При анализе динамического ряда необходимо выяснить, какими абсолютными значениями выражаются темпы роста, темпы прироста уровня, так как в некоторых случаях при снижении (замедлении) темпов роста абсолютный прирост может возрастать. Поэтому при анализе динамического ряда в статистике вычисляется абсолютное значение одного процента прироста (снижения).

Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:

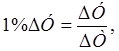(2.12)

После несложного преобразования формулы получим:

(2.13)

Это означает, что абсолютное значение одного процента прироста (снижения) равно 0,01 базисного уровня.

Проведем расчет вышеперечисленных показателей в таблице 2.1.

Таблица 2.1. Показатели динамики уровня оплаты корма (кг/т к.ед.) в сельскохозяйственной организации за 2005 – 2009 г.г.

Данные таблицы 2.1 свидетельствуют о том, что уровень оплаты кормов в 2006 и 2007 гг. по сравнению с 2005 годом увеличились на 1 и 13 кг/т к.ед. соответственно, в 2008 году по сравнению с 2005 годом – уровень оплаты корма пошел на спад (-6 кг/т к.ед.).

Темп роста в среднем составил 106,9 %, а абсолютное значение в среднем составило 1 кг/т. к.ед.

Выявление общей тенденции развития признака может быть проведено с использованием приемов аналитического выравнивания динамического ряда. Аналитическое выравнивание ряда динамики обычно осуществляется следующими способами: по прямой линии; по гиперболе; по параболе второго порядка.

Способы аналитического выравнивания хотя и содержат в себе ряд условностей, но более совершенны по сравнению с укрупнением периодов и скользящей средней. Аналитическое выравнивание облегчает выявление общей тенденции и изучение сезонных колебаний в характере динамического ряда. Выбор того или иного способа аналитического выравнивания обусловлен характером (типом) динамики. Характер динамики может быть выражен в виде аналитических уровней, которым на координатном графике соответствует определенная линия — прямая, парабола, гипербола и т. п.

Тип динамики целесообразно учитывать при выборе способов аналитического выравнивания динамических рядов. Если динамический ряд имеет более или менее стабильные абсолютные приросты, то выравниваемый динамический ряд может быть выражен в виде прямой линии. При этом на координатном графике фактические уровни ряда наиболее целесообразно показать прямолинейно.

При выравнивании по прямой линии закономерно изменяющийся уровень признака рассчитывается как функция времени:

(2.14)

где Уt - выровненные значения уровней ряда;

t - периоды или моменты времени, к которым относятся уровни;

а, b - параметры уравнения (искомой прямой).

Для расчета параметров уравнения прямой линии обычно применяют способ наименьших квадратов, в основе которого лежит следующее требование: сумма квадратов отклонений фактических уровней ряда (У) от выровненных