Уровень ряда, который сравнивается с базисным, называется текущим (отчетным). Текущие уровни могут иметь следующие обозначения: У1, У2, У3 .Уn.

Если все уровни динамического ряда сравниваются с одним и тем же базисным уровнем, то полученные показатели динамики называются базисными. Если же каждый последующий уровень ряда сравнивается с каждым предыдущим, то полученные динамические показатели называются цепными. Они представляют собой как бы отдельные звенья единой «цепи», связывающей между собой уровни ряда.

Выбор базы сравнения при построении и анализе динамических рядов может быть обоснован экономическими или историческими особенностями развития изучаемого явления.

В динамическом ряду обычно приводится несколько последовательных уровней, среди которых особый интерес представляет начальный, конечный и средний. Первый член динамического ряда называется начальным, а последний его член — конечным уровнем. Для общей характеристики явления за весь период может быть исчислен средний уровень из всех членов ряда динамики. Средний уровень динамического ряда называется хронологической средней.

Одним из наиболее простых показателей динамики является абсолютный прирост уровня. Абсолютным приростом называется разность двух уровней периодического ряда динамики. Он измеряется в тех же единицах, в которых показаны абсолютные уровни ряда динамики. Если абсолютный прирост уровня обозначим через ΔУ, уровень отчетного периода У1, уровень базисного (начального) периода Уо, то абсолютный прирост может быть выражен следующим образом:

ΔУ=У1-Уо. (2.1)

Абсолютный прирост выражает абсолютную скорость роста и показывает, на сколько единиц увеличился или уменьшился отчетный уровень динамического ряда по сравнению с базисным.

Характер динамического ряда может принимать разнообразные формы. Если уровни ряда динамики от начального к конечному увеличиваются, то такой динамический ряд будет иметь абсолютный прирост. В тех случаях, когда каждый последующий уровень ряда ниже предыдущего (базисного), имеет место не абсолютный прирост, а абсолютное снижение уровня.

Абсолютные приросты могут быть рассчитаны базисным и цепным способами. Абсолютные приросты, полученные в результате сравнения текущих (отчетных) уровней с постоянным (базисным), называют базисными. Те приросты, которые получены при сравнении каждого последующего уровня с предыдущим, называются цепными.

В статистико-экономических исследованиях динамики явлений часто приходится рассчитывать средний абсолютный прирост уровня динамического ряда.

Средний абсолютный прирост всегда является периодическим показателем. Поэтому он исчисляется по формуле простой арифметической из цепных абсолютных приростов за последовательные и более-менее равные по продолжительности периоды:

ΔУ=ΣΔУц/n; (2.2)

где ΔУ — средний абсолютный прирост;

n — число цепных приростов.

Сумма цепных абсолютных приростов (ΣΔУц) ряда динамики представляет собой абсолютный прирост за весь изучаемый период в целом (Уn—У0), а число приростов (n) равно численности тех единиц времени, за которые исчисляется средний абсолютный прирост. Число приростов (длина периода) равно разности между «хронологическими номерами» конечного и базисного уровней динамического ряда, или числу членов ряда минус единица (m—1). Следовательно, формулу среднего абсолютного прироста можно выразить в следующем виде:

(2.3)

где Уn – значение конечного уровня динамического ряда;

Уо – начальный уровень ряда;

m – число членов ряда.

Для характеристики относительной скорости изменения уровня динамического ряда используется показатель темпа роста. Темп роста — это отношение одного уровня динамичного ряда к другому, принятому за базу сравнения. Темпы роста могут быть выражены в двух формах: в виде коэффициентов или процентов.

Коэффициент роста показывает, во сколько раз сравниваемый (текущий) уровень больше базисного:

К=Уn/Уо, (2.4)

Где К — коэффициент роста уровня;

Уn - уровень текущего периода;

Уо - уровень базисного периода.

Коэффициент роста, выраженный в процентах, называется темпом:

Т=Уn/Уо*100, (2.5)

Темпы роста могут быть базисными и цепными.

Темпы роста уровней динамического ряда по периодам обычно неодинаковы, т.е. обнаруживают некоторые колебания. Вследствие этого возникает необходимость исчисления среднего темпа роста.

В отличие от показателя абсолютного прироста за весь период, который представляет собой сумму абсолютных приростов за каждый отдельный период, показатель темпа роста — это произведение цепных темпов роста за каждый промежуток времени. Поэтому для определения средних темпов роста применяют формулу средней геометрической:

(2.6)

где Т — средний темп роста;

К1, К2 — коэффициенты роста за каждый период;

n — число темпов роста.

Если произведение цепных темпов заменить соответствующим базисным темпом роста за весь изучаемый период, то получим формулу среднего темпа, имеющую следующий вид:

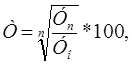(2.7)

где Т — средний темп роста;

Уn— абсолютный уровень конечного периода;

У0 — абсолютный уровень начального периода;

n — число периодов, равное числу лет минус единица (m-1).

Если абсолютная скорость прироста уровня динамического ряда характеризуется величиной абсолютного прироста, то относительная — темпом прироста.

Темп прироста — это отношение абсолютного прироста к уровню, принятому за базу. Темпы прироста, как и темпы роcта, могут быть выражены в форме коэффициентов и процентов. Коэффициент прироста показывает, на какую долю увеличился или уменьшился уровень по сравнению с базисным:

(2.8)

где ΔК — коэффициент прироста уровня, выраженный в долях;

ΔУn— значение абсолютного прироста уровня;

У0 - уровень, принятый за базу.

Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился отчетный уровень по сравнению с базисным:

ΔТ=ΔК*100 (2.9)

Темпы прироста, как и темпы роста, могут быть рассчитаны базисным и цепным способами. Между темпами прироста и темпами роста существует непосредственная связь, т.е. если темп прироста выражен в процентах, то он на 100 % меньше темпа роста:

ΔТ==Т-100 (2.10)

Темпы прироста могут быть выражены положительными (+) и отрицательными (-) значениями. Положительное значение темпа указывает на рост отчетного уровня по сравнению с базисным, отрицательное — на его снижение В последнем случае говорят о темпе снижения.

Темпы прироста за весь промежуток времени в динамическом ряду могут быть охарактеризованы при помощи их среднего значения.

При расчете среднего темпа прироста можно исходить из значения среднего темпа роста:

ΔТ==Т-100, (2.11)