Количество электронов, выброшенных в зону проводимости с уровня донорной примеси описывается соотношением

nd=Nd * (1+exp(-(Ed-F)/kT)) –1 (1)

Количество электронов, захваченных акцепторной примесью из валентной зоны описывается соотношением

na=Na * (1+exp(-(F-Ea)/kT)) –1 (2)

В этих формулах Na и Nd Эффективные плотности состояний атомов донорной и акцепторной примесей, а Ed и Ed их энергетические уровни.

Из формул (1) и (2) видно, что доля ионизированных атомов примеси зависит не только от температуры, но и от положения энергетического уровня примеси в запрещенной зоне. При фиксированной температуре ионизация примеси будет тем меньше, чем ближе ее энергетический уровень к центру заперщенной зоны.

Далее рассматривается задача с малыми концентрациями примесей. В качестве условия малости концентрации выдвигается условие, что эффективные плотности состояний каждой из примесей много меньше эффективных плотностей состояний в валентной зоне и зоне проводимости. Далее рассматриваем задачу с малыми концентрациями примесей. Количество носителей заряда в зоне проводимости полупроводника определяется как сумма носителей заряда, ионизированных с каждого из донорных уровней в отдельности. Таким образом

nd=SNdi * (1+exp(-(Edi-F)/kT)) –1 ( 3)

Далее концентрации «дырок» в валентной зоне. Можно записать аналогичное соотношение.

na=SNai * (1+exp(-(F-Eai)/kT)) –1 ( 4)

При записи выражений (3) и (4) не учтено влияние переброса носителей заряда из валентной зоны в зону проводимости. Однако можно показать, что этот вклад много меньше вклада от примесей.

Используя определение проводимости вещества j=sE , будем иметь выражение, связывающее проводимость полупроводника с концентрациями носителей заряда в нем.

s=e nd md +e na ma ( 5)

Подставляя в (5) выражения для nd и na получаем выражение для s

s=e ( md SNdi * (1+exp(-(Edi-F)/kT)) –1+ ma SNai * (1+exp(-(F-Eai)/kT)) –1)

s= (S e md Ndi * (1+exp(-(Edi-F)/kT)) –1+ S e ma Nai * (1+exp(-(F-Eai)/kT)) –1)

Обозначая

sdi =e md Ndi * (1+exp(-(Edi-F)/kT)) –1

sai =e ma Nai * (1+exp(-(F-Eai)/kT)) –1

Преобразуем выражение для s к виду

s= Ssdi + Ssai ( 6)

В последнем выражении величины sdi и sai являются проводимостями, обусловленными ионизацией i-ой донорной или акцепторной примеси (далее эти величины называются парциальными проводимостями ). Таким образом суммарная проводимость полупроводника рассчитывается как сумма парциальных проводимостей от каждой из примесей.

Зависимость количества адсорбированных молекул от температуры.

Ударяясь о поверхность твердого тела молекулы газа адсорбируются. Время адсорбции или пребывания молекул в адсорбированном состоянии зависит от теплоты адсорбции и описывается уравнением Френкеля

ta=t0 exp(Qa/RT) (7)

Где t0-минимальное время пребывания молекулы в адсорбированном состоянии. По порядку величины t0 соответствует значению 10-13 с. Qa –теплота адсорбции, рассчитанная на моль газа.

Основные составляющие воздуха имеют теплоты адсорбции на различных поверхностях в пределах от 10 до 20 кДж/кмоль. Время их адсорбции при комнатной температуре составляет порядка 10-10 с

Для нахождения зависимости количества адсорбированных молекул от температуры воспользуемся условием постоянства степени покрытия (отношения площади адсорбированных молекул к площади поверхности адсорбирующего тела).

(8)

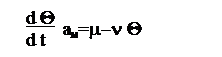Условие адсорбционного равновесия на поверхности заключается в равенстве скоростей испарения и конденсации молекул. Величина aм количество молекул, необходимое для образования монослоя на поверхности твердого тела.

(9)

Где Qстепень покрытия поверхности. Из последнего уравнения следует.

Q=m/n (10)

Величина nопределяется как скорость испарения газа с поверхности, покрытой мономолекулярным слоем.

n= aм/ta (11)

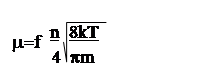Значение m определяется как количество ударившихся о поверхность молекул, помноженное на вероятность поглощения молекулы газа на поверхности

(12)

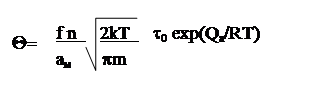Подставляя (12) и (11) в (10) и учитывая выражение для ta имеем

(13)

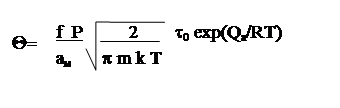Подставляя в (13) выражение для n = P / (kT) получаем окончательное выражение

(14)

Для определения количества примесных носителей заряда в полупроводниковой пленке, адсорбировавшей примесь необходимо подставить в (3) и (4) выражения для количества атомов примесей, полученные из (14)

Предполагая независимость f от температуры получаем.

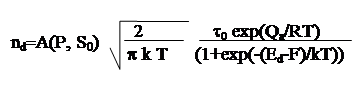Nd=Q S0

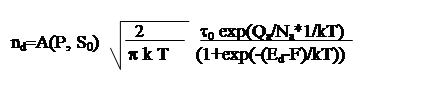(15)

В последнем выражении A(P, S0) независящая от температуры и свойств полупроводника константа. Na –постоянная Авогадро. Из последнего выражения видно, что на количество электронов в зоне проводимости оказывают влияние два конкурирующих процесса – выброс электронов в зону проводимости, увеличивающийся с ростом температуры, и уменьшение количества примесных уровней с ростом температуры. В приложении приведены графики зависимости (15) как функции температуры для различных значений параметра (Ed-F).

Принципы обработки сигналов сенсора

Гипотеза линейной аддитивности сигналов.

Очевидно, что чем больше концентрация молекул в окружающем газе, тем больше число молекул, абсорбированных на поверхности тонкопленочного чувствительного элемента сенсора, и тем больше изменение его электропроводности. Ясно также, что при представляющих интерес концентрациях примесей, степень покрытия поверхности сенсора много меньше единицы. В этих предположениях изменение s электропроводности (чувствительного элемента сенсора при появлении в окружающем сенсор газе примесей с концентрацией C ) можно считать связанными линейно и аддитивно, т.е. полагать, что

S Cisi = s (16)

где суммирование идет по видам примесей, si - соответствующие коэффициенты пропорциональности. Коэффициенты si зависят от температуры, это обуславливает суммарную зависимость от температуры электропроводности чувствительного элемента сенсора.

Соотношение (16) выражает содержание гипотезы линейной аддитивности результирующей термограммы: предполагается, что наблюдаемая зависимость s(Т) есть сумма "парциальных" проводимостей, каждая из которых отражает вклад отдельной примеси в окружающем газе в суммарную электропроводность чувствительного элемента сенсора.