Метод волновых фронтов (полей времен)

а) Метод Торнберга. Целый ряд способов интерпретации данных МПВ, как правило графических, основан на реконструкции волновых фронтов.

Рис. 7 иллюстрирует принцип метода построения волновых фронтов. Фронт преломленной волны, достигающий точки А в момент времени t = 1,600 с, подходит к В, С, . в моменты 1,600 + DtB, 1,600 + Dtc, Построив дуги окружностей с центрами В, С, . и радиусами V1 DtB, V1 DtC,,… , мы можем восстановить волновой фронт для t = 1,600 с (AZ) с требуемой точностью. Подобным же образом можно построить волновые фронты для любого момента времени (см., например, приведенный на том же рисунке волновой фронт для t = 1,400 с) Показаны также волновые фронты прямой волны от источника S, являющиеся окружностями.

На рис. 8 изображены только те фронты, которые соответствуют волнам, приходящим первыми (все последующие вступления для простоты исключены из рассмотрения). В интервале между источником S и точкой выхода преломленной волны С в первых вступлениях наблюдается прямая волна. Вправо от С первой приходит волна, преломленная на первой границе, но вправо от G ее обгоняет волна, преломленная на более глубокой границе.

Две системы волновых фронтов, соответствующие прямой волне и волне, преломленной на первой границе, пересекаются

Рис. 7. Построение волновых фронтов.

вдоль пунктирной линии ABC; эта линия, названная Торнбергом кривой совпадения времен, проходит через точки, где пересекающиеся волновые фронты характеризуются одинаковым временем. DEFG — кривая совпадения времен для более глубокой границы. Кривые совпадения времен касаются преломляющих границ в точках А и D, где угол падения луча достигает критического значения, а точки, в которых кривые совпадения времен пересекают поверхность, отличаются резким изменением наклона годографа.

Поскольку кривая совпадения времен касается преломляющей границы, положение последней можно найти, если есть данные по одному профилю плюс некоторые дополнительные данные, например ее наклон, глубина, критический угол, или же данные еще по одному профилю (не обязательно встречному), так как в этом случае есть две кривые совпадения времен и преломляющая граница является для них общей касательной.

Если есть данные по встречным профилям, построение волновых фронтов позволяет реализовать изящный метод построения преломляющей границы. Суть метода ясна из рис. 9,

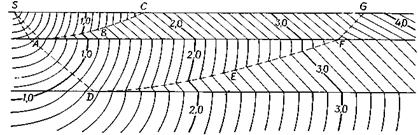
Рис. 9.Кривые совпадения времен.

на котором показаны два волновых фронта MCD и РСЕ, построенных из точек А и В и пересекающихся в промежуточной точке С. Очевидно, что сумма времен пробега от А и В до С равна взаимному времени tr для пунктов взрыва А и В. Если построить два волновых фронта по годографу, не зная положения преломляющей границы RS, они будут выглядеть как MCN

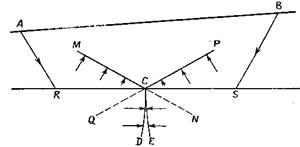
Рис. 9.Построение преломляющей границы по точкам пересечения волновых фронтов.

и PCQ, а не как MCD и РСЕ. Следовательно, если начертить пары волновых фронтов из А и В, таких, что сумма времен пробега равна tr, преломляющая граница будет проходить через точки пересечения соответствующих пар волновых фронтов на рис. 9.

б) Метод «плюс-минус» Хагедорна. В методе «плюс-минус» Хагедорна применяется построение, сходное с вышеописанным. Когда преломляющая граница горизонтальна, пересекающиеся волновые фронты, проведенные с интервалом D мс, образуют ромбовидные фигуры (рис. 10), горизонтальные и вертикальные диагонали которых равны V2D и V1D/cosQ соответственно. Если сложить два значения времени пробега на любом пересечении и вычесть t0, то полученный результат (значение «плюс») будет равен нулю на преломляющей границе,

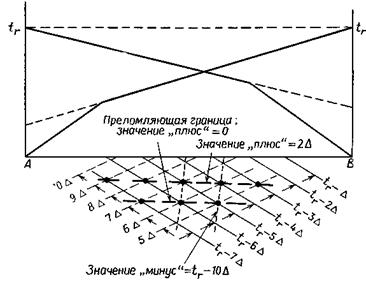
Рис. 10. Интерпретация по методу «плюс-минус:

+2D на горизонтальной прямой, проходящей через предыдущий ряд значений по вертикали над теми пересечениями, которые определяют преломляющую границу, +4D на следующей линии пересечений вверх по разрезу и т. д. Поскольку расстояние между каждой парой соседних линий составляет V1D/cosQ, для построения преломляющей границы можно использовать любую из «плюс»-линий. Разность между двумя временами в точке пересечения называется значением «минус»; она постоянна вдоль субвертикальных линий, проходящих через пересечения волновых фронтов. Расстояние между последовательными «минус»-линиями, как следует из рис. 10, составляет V2D; благодаря этому можно непрерывно контролировать значение V2. Несмотря на то что наклон границы изменяет приведенные соотношения, в случае небольших углов наклона искажения достаточно малы; поэтому считается, что «плюс»-линии остаются параллельными преломляющей границе, а «минус»-линии не сходятся и не расходятся по отношению друг к другу.

в) Графический метод Хейлса. Графические способы очень удобны для решения многих задач интерпретации в методе преломленных волн. При аккуратном выполнении графические построения обычно позволяют быстро получить решение с требуемой точностью, и ими удобно пользоваться, так как интерпретация отличается наглядностью.

Метод Хейлса полезен в тех случаях, когда заметно меняется глубина преломляющей границы; такая ситуация часто связана с изменениями скоростей в покрывающей толще, а также граничных скоростей. Для применения этого метода нужны встречные годографы. Сущность его в использовании сопряженных точек, скажем А и В (рис. 11, а), расположение которых соответствует общей точке Q отхода волны от границы; при этом глубина и наклон преломляющей границы заранее не известны. Сначала мы опишем процесс интерпретации, а затем докажем сделанные предположения.

На данной паре встречных годографов, подобных приведенным на рис. 11, б, выбираем произвольную точку В, в которой время прихода волны равно tRB. Точка К определяется соотношением KB = tr — tRB. Прямая, проходящая через К под углом a = arctg(V1sinQ), отсекает на встречном годографе время tSA в положении А, которое является точкой на встречном профиле, связанной с той же точкой на преломляющей границе (Q на рис. 11, а), что и В. Теперь можно определить время t’ и расстояние x’(рис. 11, б) по встречному годографу. Проводим прямую через А под критическим углом Q (рис. 11, в), которая пересекает в точке С перпендикуляр, восстановленный в середине отрезка АВ. Затем проводим дугу радиуса r = V1t’/2cosQ. Преломляющую границу строим как огибающую дуг, проведенных таким путем. Угол a, введенный выше, не точно равен углу a', но, как будет показано, этой ошибкой можно пренебречь.

Чтобы доказать провильность построений этого метода, рассмотрим треугольник AQB (рис. 11, г), где Q — точка преломления. Преломленные волны, распространяющиеся от R до В и от S до А (рис. 11, а), отходят от преломляющей границы в точке Q. Проведем окружность через точки A, Q и В, после чего значения ряда углов можно выразить через критический угол Q и угол наклона границы x. Расстояние CQ = r можно найти, если учесть, что