Расчет динамики подземных вод
![]() (23)
(23)
Выражение ![]() можно записать так
можно записать так
![]() (24)
(24)
т. е. единичный расход равен
![]() (25)
(25)
а полный расход составит
![]() (26)
(26)
Исследуя выражение (22), мы сможем решить одну из весьма важных задач в гидрогеологических расчетах — вывести уравнение депрессионной кривой. Построение депрессионной кривой необходимо при возникновении угрозы затопления подземными водами котлованов, подвалов зданий и т. п
Изменив пределы интегрирования в выражении (20) по X от 0 до х, а по У от h0 до h К получим
![]() (27)
(27)
Естественно, что приток воды в выражениях (22) и (27) одинаков, т. е.
![]() (28)
(28)
Решаем (28) относительно h
![]() (29)
(29)
Для построения депрессионной кривой мы задаемся величиной hо в зависимости от 5, мощность водоносного горизонта H легко получить по данным бурения, величину радиуса влияния можно найти по эмпирическим формулам (об этом мы поговорим позже).
На миллиметровой бумаге строим разрез через дрену и котлован (рис. 52) и, задаваясь разными значениями х(хи x2, ., хп), например 10, 20, 30 и т. д. метров, получаем величины h(h, h2, ., hп). Соединив полученные точки плавной линией, получим кривую депрессии. Если она проходит через котлован, строят новую кривую, задавшись большей величиной понижения и, естественно, меньшим значением глубины воды в дрене. Построение производят до тех пор, пока депрессионная кривая не опустится ниже дна котлована.
4.2 Расчет притока грунтовых вод в скважину
Здесь мы имеем дело не с плоским потоком, как в предыдущем примере, а с радиальным. На рис. 10 показаны все обозначения, которые нам ясны из предыдущей задачи, кроме г — радиуса скважины.
Расчет начинаем с уравнения (13). Площадь притока воды равна площади боковой поверхности цилиндра, радиус которого равен х, т. е.
![]() (30)
(30)
![]() (31)
(31)
Разделяем переменные (т. е. умножаем обе части уравнения на ![]() ) и интегрируем
) и интегрируем
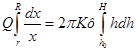 (32)
(32)
Интегрирование по х производим не от нуля, а от r — стенки скважины, в результате получаем формулу Дюпюи
![]() (33)
(33)
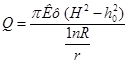 (34)
(34)
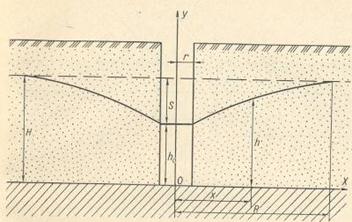
Рис. 2. Схема притока грунтовых вод в совершенную скважину
В таком виде использовать выражение (2) не совсем удобно, так как в нем присутствует натуральный логарифм. Подставим вместо него десятичный (1nх = 2,30 lgх), а вместо л его значение и получим более удобное выражение для расчета притока безнапорных вод в скважину:
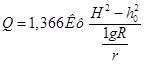 (35)
(35)
Выражение ![]() можно видоизменить:
можно видоизменить:
![]() (36)
(36)
И, подставив его в зависимость 54), получим
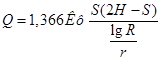 (37)
(37)
Для построения депрессионной кривой возвращаемся к (35) и изменяем пределы интегрирования: по X от r до х а по Y от h0 до h:
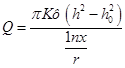 (38)
(38)
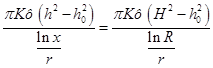 (39)
(39)
 (40)
(40)
Решаем равенство относительно h и получаем уравнение кривой депрессии
 (41)
(41)
4.3 Расчет притока напорных вод в совершенную дрену
Площадь фильтрации в сечении h, расположенном на расстоянии х от стенки дрены, будет равна
![]() (42)
(42)
Мы здесь снова не учитываем приток воды через торцы дрены. Подставляем площадь в (43):
![]() (43)
(43)
Переходим к единичному расходу
![]() (44)
(44)
Разделяя переменные и интегрируя, получим
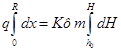 (45)
(45)
![]() (46)
(46)
![]() (47)
(47)
Выражение (47) представляет собой единичный приток артезианских вод в один из бортов канавы. Полный приток составит
![]() (48)
(48)
Если нам необходимо получить уравнение депрессионной кривой, то (43) нужно проинтегрировать по Х от 0 до ж, а по Y от hо до h:
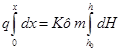 (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
Решаем уравнение (51) относительно h:
![]() (52)
(52)
Анализируя выражение (52), мы видим, что это уравнение прямой линии. На самом деле депрессионная кривая криволинейна.
4.4 Расчет притока артезианских вод в скважину
В выражение (14) подставляем величину площади фильтрации, которая равна
![]() (53)
(53)
![]() (54)
(54)
Разделяя переменные и интегрируя по X от r до Н, а по Y от hо до Н, получим
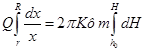 (55)
(55)
![]() (56)
(56)
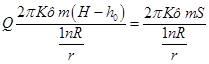 (57)
(57)
Переведем натуральный логарифм в десятичный и подставим значение я. Получим выражение для расчета притока артезианских вод в совершенную скважину:
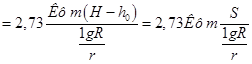 (58)
(58)
Для расчета кривой депрессии возвратимся к (55) и сменим пределы интегрирования: по X от r до х,а по Y от hо до h:
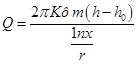 (59)
(59)
Выражения (57) и (59) равны:
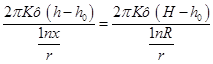 (60)
(60)
Находим h:
 (61)
(61)
т. е. мы снова имеем уравнение прямой линии, хотя в природных условиях депрессионная воронка в разрезе имеет вид кривой.
