Оптимизация профиля отражения частотных фильтров излучения с использованием модулированных сверхрешеток
Для таких полей ротор сводится к оператору qx![]() + ikbx и уравнения Максвелла (1) принимают вид
+ ikbx и уравнения Максвелла (1) принимают вид
(qx![]() + ikbx)H = -ikD(5)
+ ikbx)H = -ikD(5)
(qx![]() + ikbx)E = ikB
+ ikbx)E = ikB
Умножая уравнения (5) на вектор q, получаем соотношения
qD = aH , qB = -aE , a = b![]() q (6)
q (6)
При нормальном падении (b = 0) поле (4) представляет собой плоскую волну. Нормальные компоненты векторов электрической и магнитной индукции такой волны равны нулю: qD = qB = 0. Векторы электромагнитного поля в линейной среде связаны уравнениями
D = ![]() E , B = mH , (7)
E , B = mH , (7)
где ![]() и m - тензоры диэлектрической и магнитной проницаемостей. В общем случае поглощающей анизотропной среды, обладающей собственной или вынужденной гиротропией [9],
и m - тензоры диэлектрической и магнитной проницаемостей. В общем случае поглощающей анизотропной среды, обладающей собственной или вынужденной гиротропией [9], ![]() и m - комплексные несимметричные тензоры.
и m - комплексные несимметричные тензоры.
Уравнения связи (7) и соотношения (6) образуют систему восьми линейных скалярных уравнений для двенадцати декартовых компонент векторных функций E(z), D(z), H(z), B(z) вида (4). Поэтому лишь четыре из этих компонент линейно независимы. В качестве независимых функций удобно выбрать тангенциальные компоненты векторов напряженности электрического и магнитного полей, так как они непрерывны на границе раздела слоев. Выражая из уравнений (6) и (7) нормальные компоненты через тангенциальные составляющие и используя тождество [3] H = Ht +q![]() qH , получаем
qH , получаем
![]() = V
= V , где(8)
, где(8)
V = 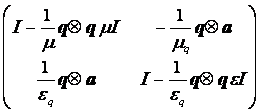 - (9)
- (9)
матрица восстановления [10] полных векторов H и E по их тангенциальным составляющим Ht и Et , а ![]() = q
= q![]() q,
q, ![]() = q
= q![]() q.
q.
С учетом соотношения (8) систему уравнений (5) можно представить в матричном виде [11]
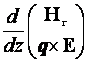 = ikM
= ikM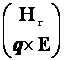 , (10)
, (10)
где
М =  (11)
(11)
- блочная матрица, составленная из операторов (12)
A = ![]() qx
qx![]() qa -
qa - ![]() bq
bq![]() I
I
B = ![]() I
I![]() I -
I - ![]() b
b![]() b (12)
b (12)
C = -![]() a
a![]() a -
a - ![]() qx
qx![]() qx
qx
D = -![]() aq
aq![]() qx -
qx - ![]() I
I![]() qb
qb
здесь ![]() и
и ![]() - тензоры, взаимные к транспонированным тензорам
- тензоры, взаимные к транспонированным тензорам
![]() и
и ![]() соответственно.
соответственно.
В прозрачных средах ![]() и
и ![]() - эрмитовы:
- эрмитовы: ![]() ,
, ![]() при вещественном параметре b имеют место равенства
при вещественном параметре b имеют место равенства
B+ = B, C+ = C, D+ = A (13)
В координатной записи уравнение (10) представляет собой систему четырех линейных дифференциальных уравнений для тангенциальных составляющих векторов H и E. Подобная система рассматривалась в [12].
Общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами выражается через экспоненциал от матрицы коэффициентов этой системы.
В нашем случае [7] имеет место
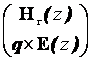 = P
= P 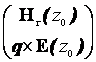 , P =
, P =  , F=
, F= (14)
(14)
Р – характеристическая матрица плоскослоистой анизотропной системы, которая связывает значения полей на первой и последней границах системы. Для системы из N-1 слоев матрицу Р можно представить в виде
Р = РN-1PN-2…PP…P1, где РР = 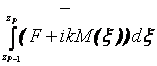 , р = 1, 2, …,N-1 – характеристическая матрица р-го слоя.
, р = 1, 2, …,N-1 – характеристическая матрица р-го слоя.
Если в пределах некоторого слоя значения функции М(![]() ) в двух произвольных точках
) в двух произвольных точках ![]() 1 и
1 и ![]() 2 коммутируют между собой, то есть
2 коммутируют между собой, то есть
М(![]() 1) М(
1) М(![]() 2) = М(
2) = М(![]() 2)М(
2)М(![]() 1) ,
1) , ![]() 1,2 Î [zP-1, zP], то матрица Р этого слоя принимает вид [7] P = exp (ik
1,2 Î [zP-1, zP], то матрица Р этого слоя принимает вид [7] P = exp (ik 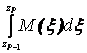 ). Для однородной среды соответствующий интеграл сводится [4] к экспоненциальному оператору
). Для однородной среды соответствующий интеграл сводится [4] к экспоненциальному оператору
