Парадоксальность этого вывода состоит в том, что в силу принципа относительности точно такая же формула должна получиться для длины масштаба, находящегося в системе S и измеряемого из системы. Иначе говоря, представляется необходимым удовлетворение обратного соотношения , которое находится в явном противоречии с (r), если под и понимать так же измеряемые величины.

Противоречие, однако, снимается, если учесть, что относительность предполагает совершенно симметричное измерение всей системы измерения, т.е. переход от предыдущего рисунка к следующему рисунку:

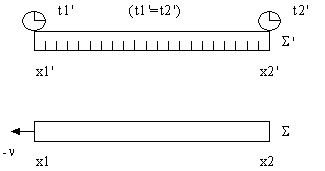
В этой схеме уже , но , т.е. концы нижнего масштаба засекаются не в один и тот же момент времени по часам, помещенным в системеS, но в один и тот же момент по часам, находящимся в системе. Тогда, применяя формулы обратных преобразований Лоренца, получаем , откуда в силу , имеем . Эта формула действительно означает, что уменьшается длина масштаба , измеренного из системы . Но эта формула уже не находится в противоречии с формулой (r), ибо входящие в нее и измеряются иначе, чем и , входящие в (r).

Следовательно, укорочение или удлинение измеряемых масштабов зависит лишь от того, в какой системе отсчета производятся одновременные измерения положений концов масштабов, ибо события, одновременные в одной системе отсчета, неодновременны в другой.

Замедление движущихся часов.

Замедление движущихся часов может быть обнаружено в следующем опыте:

Движущиеся со скоростью n часы, измеряющие время , проходят последовательно мимо точки в момент и мимо точкив момент . В эти моменты производится сравнивание положений стрелок движущихся часов и соответствующих неподвижных, находящихся с ними.

Путь за время движения от точки до точки стрелки движущихся часов отмеряют промежуток времени , а стрелки предварительно синхронизированных в неподвижной системе S часов 1 и 2 отмеряют промежуток времени t. Таким образом, (s). Но согласно обратным преобразованиям Лоренца имеем . Подставляя (s) в это уравнение и замечая, что движущиеся часы все время находятся в одной и той же точки движущейся системы отсчета, т.е. что , получаем .(u)

Эта формула означает, что промежуток времени, отмеченный неподвижными часами, оказывается большим, чем промежуток времени, отмеренный движущимися часами. Но это означает, что движущиеся часы отстают от неподвижных, т.е. их ход замедляется. Эта формула также обратима, как и соответствующая формула для масштабов. Однако написав обратную формулу в виде (t) мы должны подразумевать, что измеряются уже не в предыдущем опыте, а в следующем: (в этом случае действительно согласно преобразованиям Лоренца ) 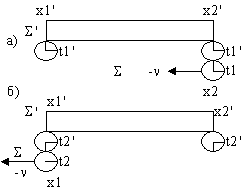при условии получаем формулу (t). Полученное замедление является вполне реальным, однако оно имеет, так сказать, чисто кинематическую природу. Например, в схеме предыдущего опыта, тот результат, что часы 2 оказались впереди движущихся часов, с точки зрения движущейся системы объясняется тем, что часы 2 с самого начала шли несинхронно с часами 1 и опережали их (в силу неодновременности разобщенных событий, одновременных в другой, движущейся системе отсчета). Таким образом, как замедление движущихся часов, так и сокращение движущихся масштабов не являются парадоксальными, если освоиться с представлением об относительности одновременности пространственно разобщенных событий.

Парадокс часов.

Более поразительным и вызывающим большое число споров и недоразумений является так называемый "парадокс часов". Путь часы А находятся в точке 1 в неподвижной инерциальной системе отсчета S , а одинаковые с ними часы В, находившиеся в начальный момент также в точке 1, движутся к точке 2 со скоростью n. Затем, пройдя путь до точки 2, часы В возвращаются и, приобретая противоположную скорость -n, возвращаются в точку 1

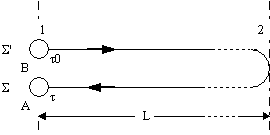
Если время, требуемое на изменение скорости часов В на обратную, достаточно мало по сравнению с временем прямолинейного и равномерного движения от точки 1 до точки 2, то время t, отмеренное часами А, и время , отмеренное часами В, можно вычислить согласно (u) по формулам (v) где d – возможная малая поправка на время ускоренного движения часов В. Следовательно, часы В, вернувшись в точку 1, реально отстанут от часов А на время Поскольку расстояние может быть сколько угодно большим, постольку поправка d может не приниматься во внимание вообще.