Вывод преобразований Лоренца без постулата о постоянстве скорости света.

Для вывода преобразований Лоренца будем опираться лишь на “естественные” допущения о свойствах пространства и времени, содержавшиеся еще в классической физике, опиравшейся на общие представления, связанные с классической механикой:

1. Изотропность пространства, т.е. все пространственные направления равноправны.

2. Однородность пространства и времени, т.е. независимость свойств пространства и времени от выбора начальных точек отсчета (начала координат и начала отсчета времени).

3. Принцип относительности, т.е. полная равноправность всех инерциальных систем отсчета.

Различные системы отсчета по-разному изображают одно и то же пространство и время как всеобщие формы существования материи. Каждое из этих изображений обладает одинаковыми свойствами. Следовательно, формулы преобразования, выражающие связь между координатами и временем в одной – “неподвижной” системе с координатами и временем в другой – “движущейся” системе , не могут быть произвольными. Установим те ограничения, которые накладывают “естественные” требования на вид функций преобразования:

1. Вследствие однородности пространства и времени преобразования должны быть линейными.

Действительно, если бы производные функций по не были бы константами, а зависели от то и разности , выражающие проекции расстояний между точками 1 и 2 в “движущейся” системе, зависели бы не только от соответствующих проекций , в “неподвижной” системе, но и от значений самих координат что противоречило бы требованию независимости свойств пространства от выбора начальных точек отсчета. Если положить, что проекции расстояний вида x‘ = = зависят только от проекций расстояний в неподвижной системе, т.е. от x = , но не зависит от , то

при т.е. или .

Аналогично можно доказать, что производные по всем другим координатам также равны константам, а следовательно, и вообще все производные по суть константы.

2. Выберем "движущуюся" систему таким образом, чтобы в начальный момент точка, изображающая ее начало координат, т.е. совпадала с точкой, изображающей начало координат "неподвижной" системы, т.е. , а скорость движения системы была бы направлена только по

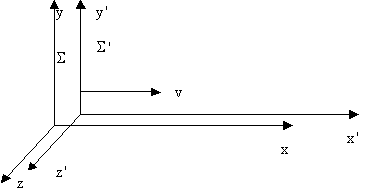
Если мы также учтем требование изотропности пространства, то линейные преобразования для системы отсчета , выбранной указанным образом, запишутся в виде Здесь отсутствуют члены, содержащие и в выражениях и , в силу изотропности пространства и наличия единственного выделенного направления вдоль оси , соответственно постановке задачи. На этом же основании в выражениях для и отсутствуют члены, пропорциональные, соответственно, и , а коэффициенты при и одинаковы. Члены, содержащие и , отсутствуют в выражениях для и в силу того, что ось все время совпадает с осью . Последнее было бы невозможно, если бы и зависели от и .

3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки и , т.е. одновременно изменить направление оси и направление движения системы . Следовательно, (d) Сравнивая эти уравнения с предыдущими () получаем: . Вместо удобно ввести другую функцию , так, чтобы выражалось через ипосредством соотношения Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде (e), причем все входящие в эти формулы коэффициенты суть симметрии функции .