Известны двуместные операции: соединение, сложение, различные виды умножений графов и др. Такие операции используются для анализа и синтеза графов с заданными свойствами.

28. Два графа G1=(V1;E1), G2=(V2;E2),называются изоморфными, если существует взаимнооднозначное соответствие между множествами вершин V1 и V2 и между множествами рёбер Е1 и Е2, такое, чтобы сохранялось отношение инцидентности.

Понятие изоморфизма для графов имеет наглядное толкование. Представим рёбра графов эластичными нитями, связывающими узлы – вершины. Тогда, изоморфизм можно представить как перемещение узлов и растяжение нитей. Теорема 1.

Пусть задан граф G=(V;E),где V - множество вершин, E - множество рёбер, тогда 2[E]=Σ(V), т.е. удвоенное количество рёбер равно сумме степеней вершин.

Теорема 2. (Лемма о рукопожатиях)

В конечном графе число вершин нечетной степени чётно.

Теорема 3.

Граф связен тогда и только тогда, когда множество его вершин нельзя разбить на два непустых подмножества так, чтобы обе граничные точки каждого ребра находились в одном и том же множестве.

Расстоянием между двумя вершинами связного графа называется длина кратчайшей цепи, связывающей эти вершины (в количестве рёбер).

Свойства связных графов.

1. Связный граф остается связным после удаления ребра тогда и только тогда, когда это ребро содержится в цикле.

2. Связный граф , имеющий К вершин , содержит по крайней мере К-1 ребро.

3. В связном графе любые две простые цепи максимальной длины имеет по крайней мере одну общую вершину.

4. В графе с N вершинами и К компонентами связности число рёбер не превышает 1/2(N-K)(N-K+1).

5. Пусть у графа G есть N вершин . Пусть D(G)- минимальная из степеней вершин этого графа . Тогда D(G) > 1/2 (N-1).

29. Связный граф без циклов называется деревом.

Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярные генеалогические деревья.

Пример(генеалогическое дерево): На рисунке показано библейское генеалогическое дерево.

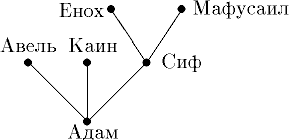
Эквивалентные определения дерева.

1. Связный граф называется деревом, если он не имеет циклов.

2. Содержит N-1 ребро и не имеет циклов.

3. Связный и содержит N-1 ребро.

4. Связный и удаление одного любого ребра делает его несвязным.

5. Любая пара вершин соединяется единственной цепью.

6. Не имеет циклов и добавление одного ребра между любыми двумя вершинами приводит к появлению одного и только одного цикла.

Раскраска графов

Раскраской графа G = (V,E) называется отображение D: V® N .Раскраска называется правильной, если образы любых двух смежных вершин различны: D (U) ≠ D (V), если (U,V) Î I. Хроматическим числом графа называется минимальное количество красок, необходимое для правильной раскраски графа.

Теорема 5.

Граф является планарным тогда и только тогда, когда он не содержит подграфа, изоморфного одному из следующих (графы Понтрягина - Куратовского).

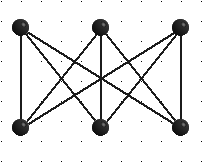Свойство: В любом планарном графе существует вершина, степень которой<=5.

Способы задания графов:

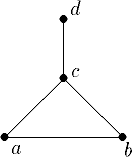1. Геометрический:

2. Матрица смежности:

Матрица смежности - квадратная матрица, размерности, равной количеству вершин. При этом а[ i, j ]-целое число, равное количеству рёбер, связывающих

i-ю, j-ю вершину. Если в графе нет петель, то диагональные элементы равны 0 .

Если рёбра не повторяются, то все элементы 0 или 1. Если граф неориентированный, то матрица симметрична.

3. Матрица инцидентности:

4. Явное задание графа как алгебраической системы:

<{a,b,c,d},{u,v,w,x}; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>.

Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d}; {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v1,v2) и (v2,v1), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его мы и будем отождествлять с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как пару (V,E), где V – множество вершин, а E – множество рёбер.