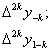Построение интерполяционного многочлена и вычисление по нему значения функции для заданного аргументаРефераты >> Программирование и компьютеры >> Построение интерполяционного многочлена и вычисление по нему значения функции для заданного аргумента
Принимаем 
=0,85; 
=0,9; 
=0,874.
Тогда 
=0,8273695; =0,8075238, и, далее, так как шаг таблицы 
=0,05, то
Т а б л и ц а 2
|
x |
|
|
|
|
|
|
|
0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00 |
0.9120049 0.8971316 0.8812009 0.8642423 0.8462874 0.8273695 0.8075238 0.7867871 0.7651977 |
-0.0148733 -0.0159307 -0.0169586 -0.0179549 -0.0189179 -0.0198457 -0.0207367 -0.0215894 |
-0.0010574 -0.0010279 -0.0009963 -0.0009630 -0.0009278 -0.0008910 -0.0008527 |
0.0000295 0.0000316 0.0000333 0.0000352 0.0000368 0.0000383 |
0.0000021 0.0000017 0.0000019 0.0000014 0.0000015 |
-0.0000004 0.0000002 -0.0000005 0.0000001
|
Т а б л и ц а 2
|
Эверетта | ||
|
|
|
|
|
0 1 2 |
0.52000 -0.06323 0.01179 |
0.82273695 -0.0009278 0.0000014 |
|
0 1 2 |
0.48000 -0.06157 0.01160 |
0.8075238 -0.0008910 0.0000015 |
|
| ||
Все вычисления по формуле Эверетта представлены в табл. 2.
Все необходимые значения разностей(и самой функции, которые мы в табл. 2 обозначили как разности нулевого порядка 
) взяты из табл. 1. Первые три строки в табл. 2 заполнены значениями 
для 
и 
, а последующие три строки соответственно значениями 
для 
и 
.
Перемножив (не снимая промежуточных результатов) коэффициенты 
на расположенные в той же строке 
, мы и получим искомое значение функции 
, как сумму произведений
Проверка производится непосредственно при помощи степенного ряда для рассматриваемой функции Эверетта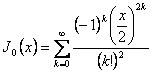 
согласно которому получим 
ГЛАВА №2
MAIN
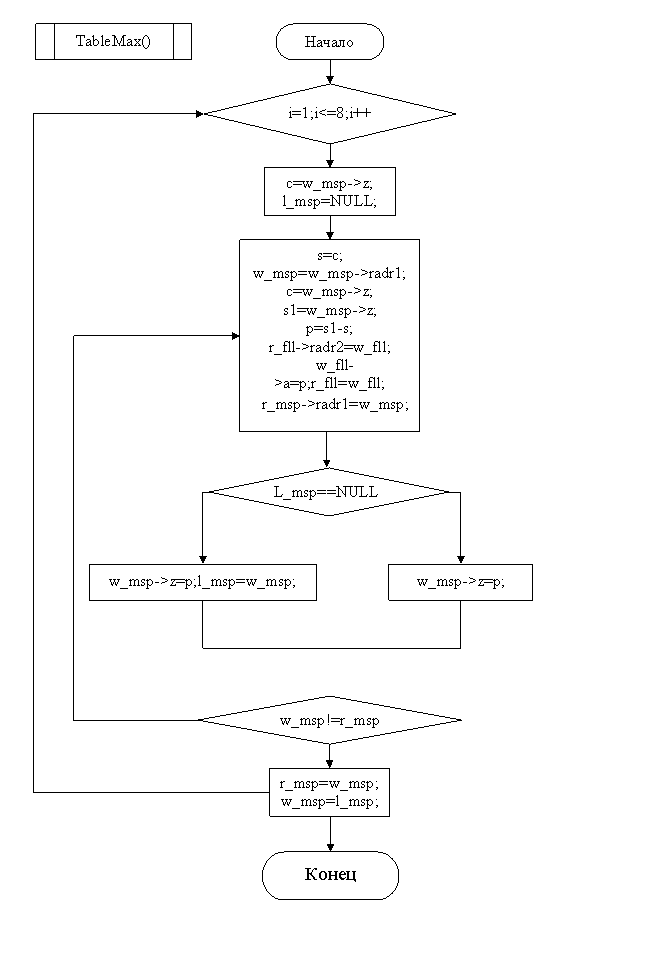
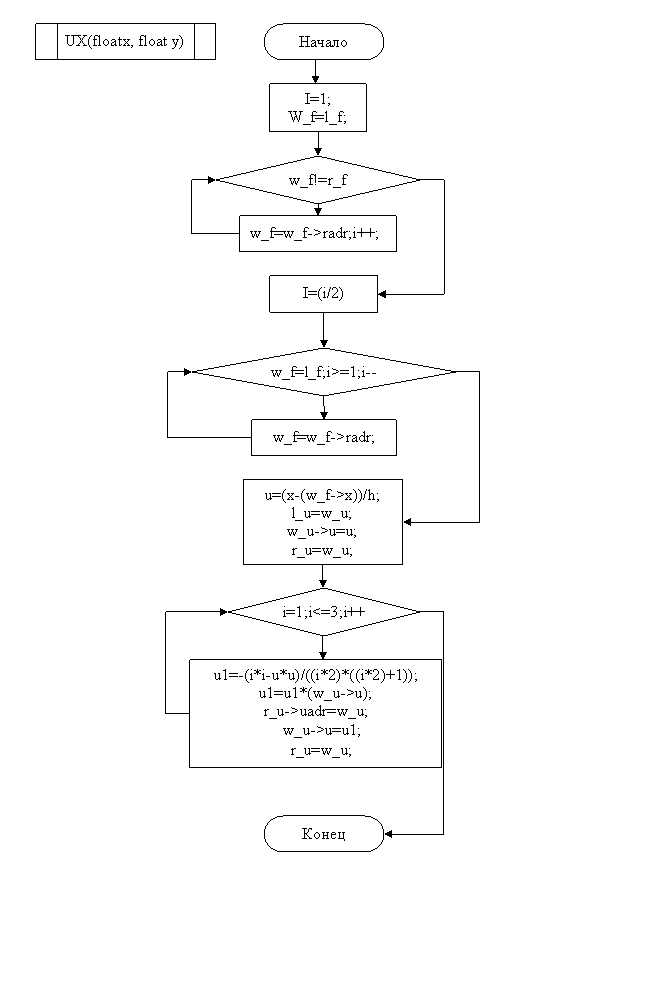
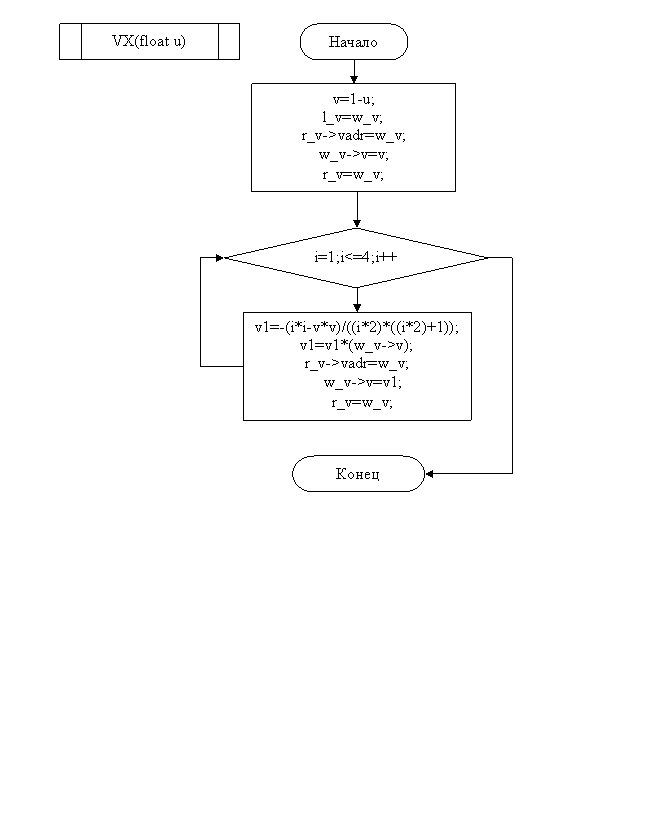
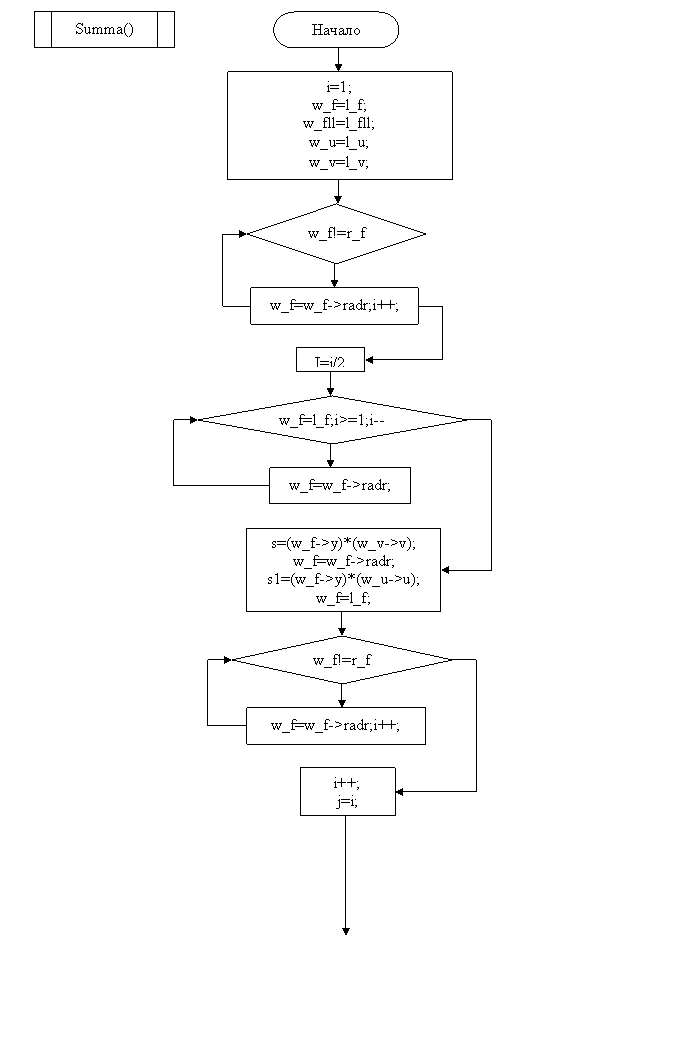
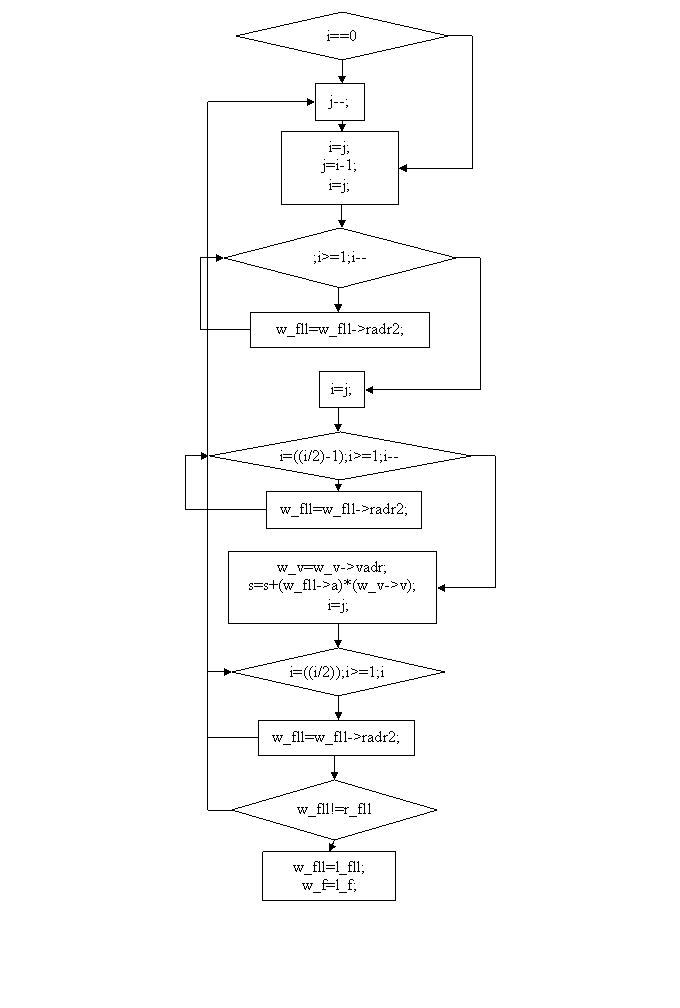
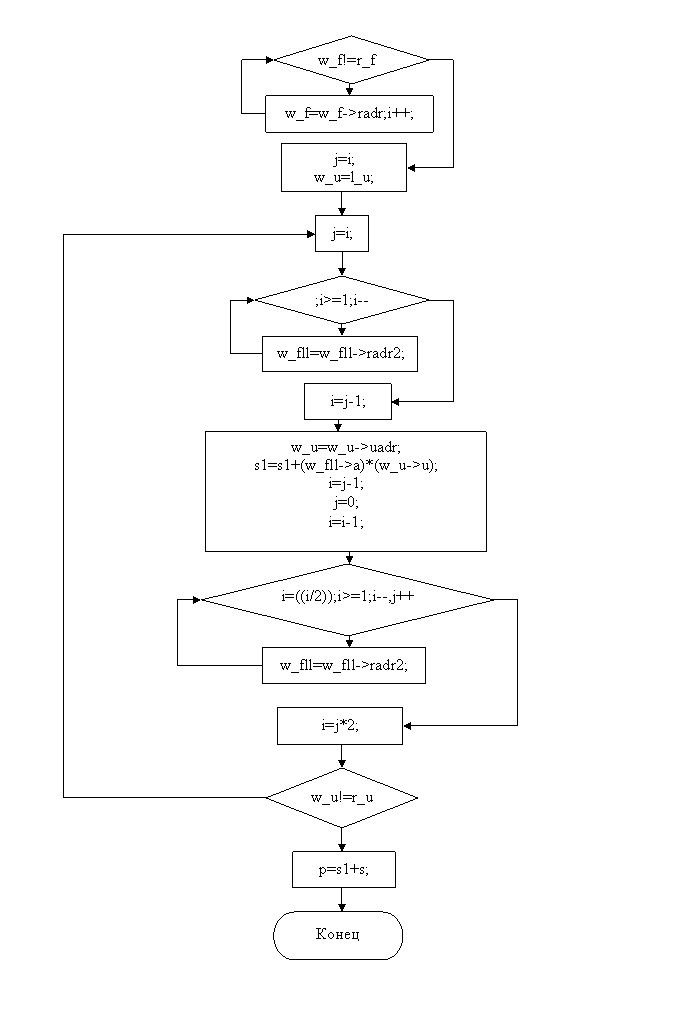
Заключение
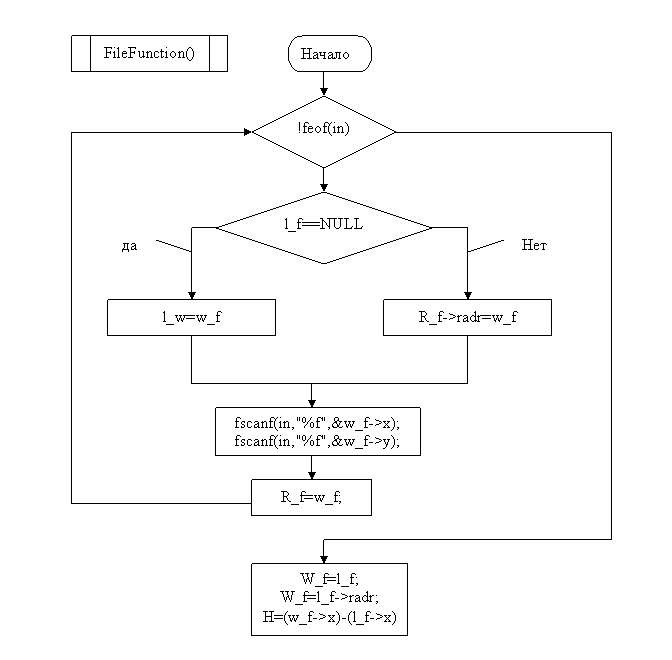
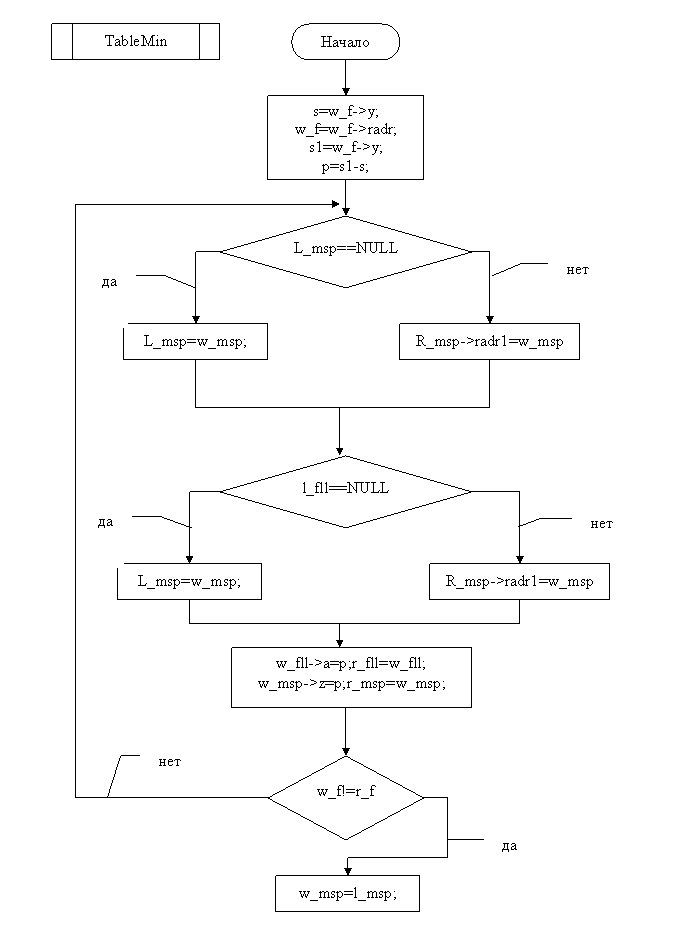
Удалось построить интерполяционный многочлен и вычислить по нему значение функции для заданного значения аргумента. Составлена блок схема алгоритма и программа на языке С++ (Приложение) для вычисления заданного интерполяционного многочлена. В программе предусмотрена возможность ввода любого числа значений функции для чего организованно хранение ее значения при помощи линейного списка.
Список литературы
1. Архангельский Н.А. Вычислительные методы алгебры в приемах и задачах. М.: МАИ, 1976.
2. Васильев Ф.П. Численные методы решения экстремальных задачь. М.: Наука,1988.
3. Васильков Ф.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. Пособие. М.: Финансы и статистика, 1999.
4. Фильчаков П.Ф., Справочник по высшей математике. Киев: Наукова думка, 1974.
5. Фильчаков П.Ф., Численные методы. Киев: Наукова думка, 1976.
6. Большая математическая энциклопедия. М.: Олма-Пресс, 2004
7. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
8. Тихонов А.Н., Вводные лекции по прикладной математике. М.: Наука, 1984.
9. Калиткин Н.Н., Численные методы. М.: Наука, 1987.
10. Корн Г., Корн Т. Справочник по математике. М.: Наука, 1984.
