Помимо этого Лапласу принадлежит барометрическая формула для вычисления изменения плотности воздуха с высотой над поверхностью земли, учитывающую влияние влажности воздуха и изменения давления.

Лаплас оставил свой след и в теории вероятностей. Он является автором простейшей из теорем теории вероятности. В общем виде она доказывалась им в книге «Аналитическая теория вероятности»(1812). Один частный случай этой теоремы был известен Муавру, в связи с чем теорему Лапласа иногда называют теоремой Муавра-Лапласа. Формулировка теоремы Лапласа такова: пусть для любого из независимых испытаний вероятность некоторого события равна (0<<1) и пусть означает число испытаний, в которых событие фактически наступило; тогда вероятность неравенства при достаточно большом числе испытаний сколь угодно мало отличается от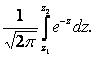

Кроме того, Лаплас имеет отношение к формулам Байеса, ныне входящим во все учебные курсы теории вероятностей. Эти формулы получаются из теоремы об умножении вероятностей при условии использования понятия полной вероятности. В действительности таких формул у Байеса нет. Его формулировка теоремы умножения воспроизводит формулировку Муавра, появившуюся в печати гораздо ранее, в 1718 г. Кроме того, у Байеса нет формулы полной вероятности. Результат, приписываемый исторической традицией Байесу, по-видимому, впервые получил привычную нам формулировку в «Опыте философии теории вероятностей» Лапласа. В главе «Общие принципы» сформулирован принцип 6, который относится к вероятностям гипотез, или вероятностям причин. Пусть некоторое событие может происходить с одним из несовместимых событий и только с ними. Эти события названы причинами. Если известно, что событие наступило, чему равна вероятность того, что осуществилась в то же время причина ? Лаплас дал такой ответ: «Вероятность существования какой-либо из этих причин равна… дроби, числитель которой есть вероятность события, вытекающего из этой причины, а знаменатель есть сумма подобных вероятностей, отнесённых ко всем причинам; если эти различные причины, рассматриваемые a priori, не одинаково вероятны, то вместо вероятности события, вытекающего из каждой причины, следует взять произведение этой вероятности на вероятность самой причины». Это и есть «правило Байеса»:

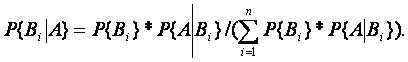
Кроме того, этот принцип Лапласа содержит и формулу полной вероятности.

Однако хотя его эпохальный труд по теории вероятностей, на первый взгляд и уводил в сторону от главных интере­сов, Лаплас вдохновлялся тем, что он был нужен математической астроно­мии. Познакомившись с этой теорией, он увидел, что она необхо­дима для всех точных наук, и посчитал оправданным развивать ее в пределах своих сил.

«Небесная механика», которая увязала все астрономические труды Лапласа в продуманное целое, публиковалась частями в те­чение 26 лет. Два тома появились в 1799 г. и касались движения планет, их формы [как вращающихся тел], приливов и отливов. Два следующие тома, вышедшие в 1802 и 1805 гг., продолжали исследование, которое было, наконец, завершено в 1823—1825 гг. пятым томом. Математическое изложение было иногда крайне сжато, а иногда громоздко. Лапласа интересовали результаты, а не то, как он их получил. Избегая сложных математических рассуж­дений, он часто опускал все, кроме заключения с оптимистиче­ским замечанием «как легко видеть». Он сам часто мог восстановить рассуждение, с помощью которого «видел» эти легкие вещи лишь после нескольких часов, а иногда и дней тяжелого труда. Даже очень сильные в математике читатели скоро приобретали привычку вздыхать во всяком месте, где появлялась знаменитая фраза, зная, что «увидеть» что-то здесь можно только после недели отчаянной работы.

Более приспособленный для чтения обзор главных результатов «Небесной механики» появился в 1796 г. в виде (ставшей класси­ческой) работы «Изложение системы мира», в которой содержалось описание лапласовского шедевра, а вся математика была опущена. В этой работе, как и в большом (153 страницы) нематематическом введении в трактат по теории вероятностей (третье издание 1820 г.), Лаплас показал себя почти таким же великим писателем, каким он был математиком. Каждый, кто хочет бегло ознакомиться с тео­рией вероятностей, не вдаваясь в технические детали, понятные только математикам, не может сделать ничего лучшего, как про­честь лапласово введение. С той поры очень много было сделано, особенно в последние годы, и главным образом в основаниях теории вероятностей, но изложение Лапласа все еще является классиче­ским, совершенным выражением, по крайней мере, одной философии всего предмета. Теория, о которой едва ли нужно здесь рассказы­вать, до сих пор еще не завершена. Более того, возникает впечатле­ние, что она еще не начиналась; следующее поколение, возможно, начнет строить ее заново.

Об одной интересной детали астрономического труда Лапласа стоит упомянуть, а именно о знаменитой гипотезе происхождения Солнечной системы из туманности. По-видимому, не зная, что его предвосхитил Кант, Лаплас (лишь полусерьезно) предложил эту гипотезу в примечании.

Речь в гипотезе идёт об образовании Солнечной системы – Солнца, планет и их спутников из вращающейся газовой туманности. Согласно гипотезе, в результате ускорения вращения при сжатии разряженная часть туманности становится всё более сплюснутой, а когда центробежная сила на экваторе стала равной по величине силе тяготения, принимает чечевицеобразную форму. Вещество на остром ребре чечевицы перестаёт участвовать в дальнейшем сжатии и остаётся на месте, образуя газовый диск. Затем он разделился на отдельные кольца, и вещество каждого кольца собралось в сгусток, превратившийся затем в планету. При сжатии этих сгустков процесс зачастую повторялся, приводя к образованию спутников планет. Центр сгущающейся туманности превратился в Солнце.

Гипотеза Лапласа не смогла объяснить медленное вращение Солнца, наличие спутников с обратным вращением и спутников, период обращения которых меньше периода вращения планет. Математика, которой он располагал, не подходила для систематического исследования вопроса, к которому не приступали, пока Джине в прошедшем столетии не резюмировал обсуждение гипотезы заявлением, что она имеет определенное на­учное значение.