После такого блестящего начала Лаплас был вознагражден пер­вой существенной почестью, будучи в возрасте лишь 24 лет, — из­бранием членом Академии наук. Его последующая научная жизнь была подытожена Фурье: «Лаплас придавал всем своим работам по­стоянное направление, от которого никогда не отклонялся; неиз­менность взглядов была всегда основной чертой его гения. Он был уже виртуозом в математическом анализе [когда занялся исследова­нием Солнечной системы], овладев всеми его тонкостями, и никто не был более компетентным, чем он, чтобы расширить эту область. Он решил главную проблему астрономии [о чем сообщил академии в 1773 г.] и посвятил весь свой талант математической астрономии, которую он был призван усовершенствовать. Он глубоко размыш­лял над своим великим проектом и всю жизнь улучшал его с настой­чивостью, уникальной в истории науки. Обширность предмета льстила гордости его гения. Он взялся написать «Альмагест» своего времени — «Небесную механику», — и его бессмертный труд по­ставил его настолько выше Птолемея, насколько аналитическая наука [математический анализ] превосходит «Начала» Евклида».

Это совершенно справедливо. Что бы Лаплас ни делал в мате­матике, все было предназначено в помощь решению грандиозной проблемы. Лаплас являет собой образец мудрости — для гениаль­ного человека — тем, что он направил все свои силы к единствен­ной центральной цели, достойной самого лучшего, чем располагает человек. Случалось, Лаплас подвергался искушению отвлечься, но ненадолго. Однажды его сильно привлекла теория чисел, но он быстро оставил ее, поняв, что ее загадки, вероятно, потребуют от него больше времени, чем он мог уделить ей, занимаясь Солнеч­ной системой.

В 1777 году, решая общие линейные уравнения с частными производными

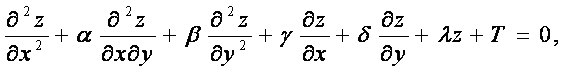
где коэффициенты и свободный член являются некоторыми функциями от х и у, создал метод решения уравнений такого рода, получивший название метода каскадов.

Сущность этого метода, как и для общего линейного дифференциального уравнения с частными производными первого порядка

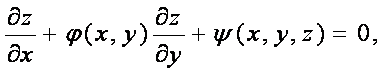
которое решал Лаплас, состоит в замене переменных. Введя две новые переменные и , Лаплас приходит к уравнению, носящему ныне его имя

или, кратко, .

Если и - две произвольные функции и если составить

то решение можно записать в виде ряда

Подстановка этого выражения в уравнение даст для определения коэффициентов дифференциальные уравнения

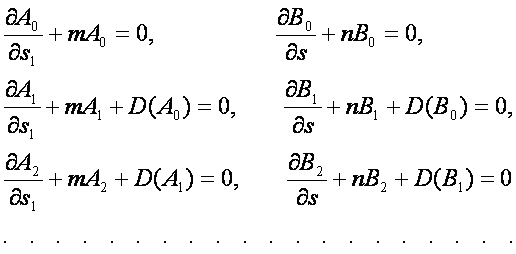
Если ряд для обрывается, т.е. для некоторого будет иметь место ,то общий интеграл выражается в конечном виде. Когда же это не имеет места, Лаплас представляет решение не рядом, а с помощью определённых интегралов. Он показал, что в этом случае

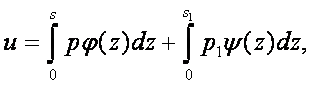
где и - частные интегралы ,

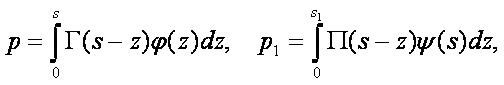
а в этих интегралах

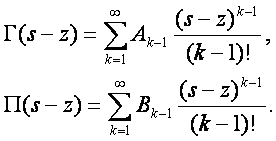
Лаплас показал, что его метод является более общим, чем все другие. В случае, например, когда - постоянные, а в уравнении :

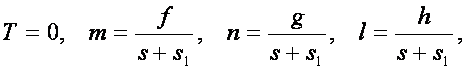
получается частный случай интегрирования обыкновенного дифференциального уравнения второго порядка. Дальнейшие усовершенствования, внесённые в метод каскадов Лагранжем и Лапласом, привели этот метод к современному виду.

Лаплас развивал метод решения линейных уравнений, разностных и дифференциальных, известный под названием преобразования Лапласа: неизвестная функция заменяется интегралом вида , или , где - новая неизвестная функция. Это преобразование переводит, как мы теперь говорим, функцию-оригинал ,, в функцию

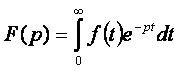
комплексного переменного Необходимые преобразования (замена переменной при интегрировании, интегрирование по направлениям, отличным от действительной оси) Лаплас ещё рассматривает как «орудия открытия», удобный метод, подобный своеобразной индукции. Его действительное значение, конечно, больше: с помощью преобразования Лапласа и аналогичных методов эффективно решаются многие задачи электротехники, гидродинамики, механики, теплопроводности, так как при этом в соответствующих линейных дифференциальных уравнениях с частными производными число переменных сокращается. Особенно широко оно применяется в операционном исчислении.

В 1779-1784 годах Лаплас занимался физикой вместе с Лавуазье, в частности вопросами о теплоте плавления тел и работами с созданным ими ледяным калориметром. Изучали горение водорода в кислороде. В 1809 году занимался вопросами акустики. Вывел формулу для скорости распространения звука в воздухе: где – среднее давление в среде, - универсальная газовая постоянная, – абсолютная температура, - молекулярный вес газа, - плотность.