Задачи и решения по прикладной математикеРефераты >> Математика >> Задачи и решения по прикладной математике
![]() = 3
= 3
Получаем третье базисное допустимое решение:
|
|
b1 =34 |
b2 =40 |
b3 =38 |
b4 =53 |
b5 =5 | |
|
Производство | ||||||
|
а1 =80 |
2 34 |
7 |
2 38 |
3 3 |
0 5 |
p1 = 0 |
|
a2 =60 |
1 |
5 40 |
4 |
2 20 |
0 |
p2 = -1 |
|
a3 =30 |
3 |
4 |
6 |
1 30 |
0 |
p3 = -2 |
|
q1 = 2 |
q2 = 6 |
q3 = 2 |
q4 = 3 |
q5 = 0 |
Находим новые потенциалы, новые оценки.
D11 = 0, p1 + q1 - c11 = 0, 0+q1 -2 = 0, q1 = 2
D13 = 0, p1 + q3 - c13 = 0, 0+q3 -2 = 0, q3 = 2
D14 = 0, p1 + q4 - c14 = 0, 0+q4 -3 = 0, q4 = 3
D24 = 0, p2 + q4 – c24 = 0, p2+3 -2 = 0, p2 = -1
D22 = 0, p2 + q2 – c22 = 0, -1+q2 -5 = 0, q2 = 6
D34 = 0, p3 + q4 – c34 = 0, p3+ 3 -1 = 0, p3 = -2
D15 = 0, p1 + q5 – c15 = 0, 0+ q5 -0 = 0, q5 = 0
Вычислим оценки свободных клеток:
D21 = p2 + q1 - c21 = -1+2-1 = 0
D31 = p3 + q1 - c31 = -2+2 -3 = -3
D12 = p1 + q2 – c12 = 0+6-7 = -1
D32 = p3 + q2 – c32 = -2+6-4 = 0
D23 = p2 + q3 – c23 = -1+2-4 = -3
D33 = p3 + q3 – c33 = -2+2-6 = -6
D25 = p2 + q5 – c25 = -1+0-0 = -1
D35 = p1 + q5 – c15 = -2+0-0 = -2
Все Dij £ 0
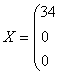
![]()
![]()
![]()
Общая стоимость всех перевозок для второго базисного допустимого решения:
L= 34*2 + 40*5 + 38*2 + 9 + 20*2+ 30 =423 – минимальная стоимость.
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕ КАПИТАЛЬНЫХ ВЛОЖЕНИЙ
Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 50 означает, что если четвёртое предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 50 тыс. руб.
Таблица 1.
|
xj |
0 100 200 300 400 500 600 700 |
|
f 1(xj) |
0 20 33 42 48 53 56 58 |
|
f 2(xj) |
0 22 37 49 59 68 76 82 |
|
f 3(xj) |
0 10 29 42 52 60 65 69 |
|
f 4(xj) |
0 16 27 37 44 48 50 56 |
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x - x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x’2(x) . Заполняем таблицу 3.
Продолжая процесс, табулируем функции F3(x), x’3(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x = 700.
Таблица 2
x - x2 0 100 200 300 400 500 600 700
F1(x - x2) 0 20 33 42 48 53 56 58
x2 f2(x2)
0 0 0 20 33 42 48 53 56 58
100 22 22* 42* 55 64 70 75 78
200 37 37 57* 70* 79 85 90
300 49 49 69 82* 91 97
400 59 59 79 92* 101*
500 68 68 88 101
600 76 76 96
700 82 82
Таблица 3
|
xj |
0 100 200 300 400 500 600 700 |
|
F2(x) |
0 22 42 57 70 82 92 101 |
|
x’2(x) |
0 100 100 200 200 300 400 400 |
Таблица 4
x - x3 0 100 200 300 400 500 600 700
F1(x - x3) 0 22 42 57 70 82 92 101
x3 f3(x3)
0 0 0 22* 42* 57* 70 82 92 101
100 10 10 32 52 67 80 92 102
200 29 29 51 71* 86* 99* 111
300 42 42 64 84 99 112*
400 52 52 74 94 109
500 60 60 82 102
600 65 65 87
700 69 69
Таблица 5
|
xj |
0 100 200 300 400 500 600 700 |
|
F3(x) |
0 22 42 57 71 86 99 112 |
|
x’3(x) |
0 0 0 0 200 200 200 300 |
Таблица 6
x - x4 0 100 200 300 400 500 600 700
F1(x - x4) 0 22 42 57 71 86 99 112
x4 f4(x4)

 Потребление
Потребление