,

где t = Т/Тс – приведенная температура, а Тс – точка Кюри.

В нулевом магнитном поле h=0 при t>1 уравнение (1.4) имеет только одно нулевое решение m=0, а приt<1 - два симметричных отличных от нуля (m¹0) решения.

На рис. 1.2 показан вид функции

m = f(h=0, t)

Точка t = 1 (или Т=Тс) является характерным примером так называемой точки бифуркации, т.е. переходу из области значений управляющего параметра (в данном случае температуры), отвечающей единственному решению уравнения, определяющего значение параметра порядка (в данном случае намагниченности), в область двух возможных значений параметра порядка.

Следует отметить, что в самой макроскопической модели никак не заложено, какое конкретно решение уравнения (1.4) будет реализовано при охлаждении парамагнитного вещества ниже точки Кюри, когда вещество начинает вести себя как ферромагнетик.

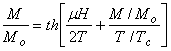(1.4)

Рис.1.2.

Процесс горения в открытой системе

Предположим, что в некоторой ячейке (реакционном объеме) может происходить экзотермическая химическая реакция

(1.5)

характеризующаяся зависящей от температуры константой скорости k(T) и тепловым эффектом Q.

Скорость выделения тепла при постоянной концентрации вещества [A], которая поддерживается за счет непрерывного притока от внешнего источника, определяется формулой

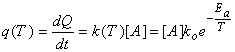(1.6)

Здесь используется обычное выражение для константы скорости химической реакции, где k0 – предэкспоненциальный множитель, Еа – энергия активации реакции.

Выделяющееся в результате реакции тепло расходуется на нагрев ячейки, а также имеет место теплообмен между ячейкой и окружающей средой. Тогда изменение температуры ячейки будет определяться следующим уравнением

(1.7)

где C - теплоемкость ячейки, g - коэффициент теплопроводности, T1 - температура среды.

В зависимости от значения параметров возможны три различных ситуации (рис.1.3). Одна из них отвечает отсутствию горения (рис. 1.3а), Т=Т1, воспламенение невозможно, единственное стационарное состояние. Другая ситуация соответствует установившемуся стационарному режиму горения Т=Т3, и избыточное тепло, выделяющееся в результате реакции, отводится в окружающую среду (рис. 1.3в). И наконец, возможна ситуация, когда уравнение f(T)=0 имеет три решения Т1<Тс<Т3 (рис. 1.3б). Состояния Т=Т1 - отсутствие горения и Т=Т3 – самовоспламенение являются стационарными, и оба устойчивы относительно малых возмущений. Однако достаточно большие возмущения могут приводить к переходу между этими состояниями и возникновению бистабильного режима.

Рис.1.3.

Ячейка может находиться либо при температуре T1 (горение отсутствует), либо при температуре T3 - стационарное горение, при котором все выделяющееся тепло отводится в среду.

Модель Шлёгля

Рассмотрим гипотетическую схему химических превращений,

(1.8)

происходящих при постоянных значениях концентраций веществ A и B. Тогда кинетическое уравнение для изменения во времени концентрации вещества Х имеет вид:

dX/dt=k1AX2- k2X3-k3X+k4B=f(X) (1.9)

Функция f(X), стоящая в правой части уравнения (1.9), является кубическим полиномом. Поэтому при определенном соотношении констант ki

возможно одновременное существование трех стационарных значений концентрации вещества X (рис.1.4), два из них, Х1 и Х3, отвечают устойчивым стационарным состояниям, а Х = Х2 является неустойчивым. Кинетическое уравнение (1.9) записано в предположении равномерного пространственного перемешивания реагирующих веществ. В реальной системе пространственные локальные флуктуации концентрации могут

Рис. 1.4.

служить малыми возмущениями. Поэтому при этих условиях возникает бистабильный режим - колебания концентрации вещества Х между двумя устойчивыми значениями Х1 и Х3.

Динамика Ферхюльста

Рассмотрим динамику изменения численности популяции исходя из следующих предположений. Пусть x0 - начальное значение численности популяции, а хn - численность популяции через n лет. Тогда относительный прирост популяции будет

Рис. 1.5.

Если R = const, то xn+1 = f(xn) = (1+R)xn = (1+R)xn = (1+R)nx0 . Пусть оптимальное значение численности популяции, которое соответствует ее равновесию со средой обитания Xопт = 1. Предположим, что относительный прирост популяции зависит от ее численности следующим образом

Rn = r(1-xn) ,

где r - параметр роста

xn+1 = f(xn) = r(1-xn)xn + xn = (1+r)xn - rxn2

Если начальное значение x0 = 0 или x0 = 1, то численность популяции со временем не изменяется, то есть x0 = 0 и x0 = 1 являются стационарными точками, причем x0 = 0 неустойчивое состояние, если r > 0. Рассмотрим устойчивость состояния x0 = 1. Пусть xn = 1 -dn , где dn - малое отклонение от состояния равновесия. Тогда

xn+1 = (1-r)(1 -dn) - r(1 -dn)2 ~ (1+r) - (1+r) dn - r + 2rdn = 1 - (1-r) dn

То есть dn+1 ~ (1-r) dn и xn+1 = 1 - dn+1

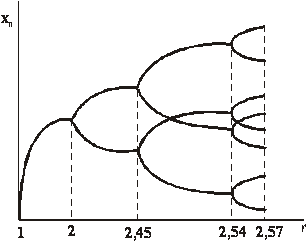Если r < 2, то ½dn+1½< ½dn½ и состояние системы устойчиво. При 2< r < Ö 6 = 2,449 происходят осциляции между двумя состояниями (рис. 1.5). При Ö6<r<2,570 динамическое поведение системы представляет собой периодическое чередование четырех различных значений численности популяций, а r>2,570 то поведение системы становится хаотичным (рис. 1.5).

В данном примере мы имеем дело с последовательными бифуркациями (рис. 1.6). При изменении параметра r сначала происходит одна бифуркация (r=2), затем при r= Ö6 на каждой из двух ветвей появляется еще одна бифуркация.

Рис. 1.6.

Список литературы

1. А.Ю. Лоскутов, А.С. Михайлов. Введение в синергетику. — М. Наука. 1990.

2. "Новое в нелинейной динамике". — Физическая мысль России. 1997. т. 2/3. 1–112 с.

3. Ф. Мун. Хаотические колебания. — М.: Мир. 1990.