В квантовой физике появляется принципиально новое понятие вероятностного предсказания поведения системы. Но и в квантовой теории сказывается влияние динамического подхода. Это проявляется хотя бы в том, что этот раздел физики чаще всего называют квантовой механикой. Вслед за А. Эйнштейном неоднократно предпринимались попытки объяснить вероятностный характер поведения квантовой системы на основе неполноты ее описания, то есть предположения о существовании скрытых динамических параметров, подчиняющихся более точной динамической теории.

В последние годы было убедительно показано не только то, что в квантовой теории принципиально не может быть скрытых локальных параметров, но и существенно изменились взгляды на классическую механику. Оказывается, что большая часть механических систем принципиально неинтегрируема. И дело даже не в том, что математики не умеют найти решение дифференциальных уравнений в конечном виде, а в том, что само поведение реальной динамической системы больше похоже на хаотическое, случайное. В физике появился новый термин - динамический хаос.

Так, например, до сих пор не получен ответ на вопрос об устойчивости солнечной системы, и специалисты склоняются к тому, что долгосрочный прогноз ее поведения невозможен. Несмотря на то, что современные компьютеры позволяют успешно управлять космическими объектами, остается верным и то, что их траектории по истечении достаточно большого времени становятся непредсказуемыми. Похожие проблемы возникают и в других областях. Невозможность адекватного представления о характере движения заряженных частиц в системе магнитных зеркал является главной причиной того, что физики до сих пор не смогли решить проблему управляемого термоядерного синтеза.

Диссипативные системы

Хаотическое поведение могут проявлять не только консервативные системы, т.е. системы у которых энергия сохраняется, но и диссипативные системы. В гамильтоновых системах, для которых справедлива теорема Лиувиля о постоянстве фазового объема, хаотичность поведения проявляется в том, что начальное состояние ансамбля систем, непрерывно заполняющее некоторую локально ограниченную область фазового пространства, с течением времени сложным образом деформируется как бы "прорастая" и заполняя все фазовое пространство. Так как фазовый объем при этом сохраняется, то со временем исходная компактная область начальных состояний ансамбля превращается в рыхлый запутанный клубок множества нитей - фазовых траекторий отдельных систем ансамбля. В диссипативных системах фазовый объем с течением времени сокращается и в самом простом случае система стремится к состоянию равновесия, а фазовая траектория имеет вид устойчивого фокуса. Если диссипативная система является отрытой и извне в систему поступает энергия, то фазовый портрет системы может иметь вид предельного цикла (система испытывает колебания), а может перейти в режим сложного стохастического движения, которое называется странным аттрактором. Таким образом, фазовые траектории диссипативных систем соответствуют аттракторам - равновесию, периодическим колебаниям или странному аттрактору.

В открытых диссипативных системах со многими аттракторами может развиваться процесс упорядочения или самоорганизации, что означает появление порядка в первоначально однородной системе.

При рассмотрении процессов пространственно-временного упорядочения в открытых диссипативных системах, находящихся в сильно неравновесном состоянии, И.Пригожин ввел термин «диссипативные структуры». Дальнейшее развитие теории диссипативных структур и неравновесных фазовых переходов позволило не только проследить глубокую аналогию с теорией равновесных фазовых переходов, но и дать более обобщенное толкование критических явлений.

Газ Ван-дер-Ваальса

Одно из наиболее известных уравнений состояния для N взаимодействующих между собой молекул газа, занимающих объем V при температуре T имеет вид

(1.1)

где P - давление, a и b - константы Ван-дер-Ваальса, характеризующие соответственно межмолекулярное притяжение и отталкивание. Нестрогий феноменологический вывод уравнения Ван-дер-Ваальса можно найти в школьном учебнике физики. Более строгий вывод с обоснованием принимаемых допущений будет подробно рассмотрен в лекции 4. Здесь отметим лишь, что межмолекулярное взаимодействие в уравнении состояния (1.1) учитывается в рамках теории самосогласованного поля.

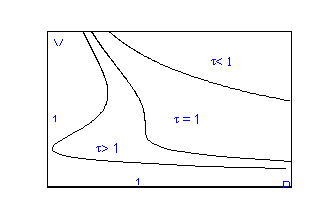
Рассмотрим зависимость удельного объема v=V/N от давления при заданном значении температуры.

(1.2)

Ясно, что удельный объем в данном случае может служить параметром, характеризующим фазовый переход газ-жидкость.

Вводя безразмерные переменные

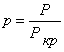
где

значения давления, объема и температуры в критической точке газ-жидкость, после соответствующего преобразования (1.1) получим следующее уравнение:

, (1.3)

решение которого дает искомую зависимость (1.2).

На рис. 1.1 показан характерный вид зависимостей v = f(p,t). При t > 1 каждому заданному значению давления соответствует одно единственное значение удельной плотности. Это означает, что при Т>Ткр есть только одно фазовое состояние газа. При t < 1 график функции f(p,t) приобретает S-образный вид, в точках p1 и p2 изотермическая сжимаемость

обращается в бесконечность, что, в частности, определяет ее сингулярное поведение.

обращается в бесконечность, что, в частности, определяет ее сингулярное поведение.

Каждому промежуточному значению р между p1 и p2 соответствует три возможных значения удельного объема системы v1<v2<v3 , из которых одно v2 не имеет

Рис. 1.1.

физического смысла, т.к. соответствует отрицательной сжимаемости, а два других определяют жидкое и газообразное состояния системы. Значение давления, при котором происходит фазовый переход для данной температуры, определяется правилом равных площадей Максвелла (см. рис. 1.1).

Магнитный фазовый переход. Точка Кюри

Рассмотрим пример перехода ферромагнетика из парамагнитного состояния в ферромагнитное состояние. Связь между намагниченностью m и внешним магнитным полем h согласно теории Кюри-Вейсса (более подробно см. лекцию 4) определяется нелинейным уравнением