Страница
1
- Функция заданная формулой y = kx + b, где k и b - некоторые числа, называется линейной.
- Областью определения линейной функции служит множество R всех действительных чисел, т.к. выражение kx + b имеет смысл при любых значениях х.
- График линейной функции y = kx + b есть прямая. Для построения графика, очевидно, достаточно двух точек, если k
 0.
0. - Коэффициент k характеризует угол, который образует прямая y = kx с положительным направлением оси Ох, поэтому k называется угловым коэффициентом. Если k > 0, то этот угол острый; если k < 0 - тупой; если k = 0, то прямая совпадает с осью Ох.
- График функции y = kx + b может быть постпоен с помощью параллельного переноса графика функции y = kx.
 Ответ №2. Опр. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax2 + bx + c, где х - независимая переменная, а, b и с - некоторые числа, причем а
Ответ №2. Опр. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax2 + bx + c, где х - независимая переменная, а, b и с - некоторые числа, причем а ![]() 0. Графиком квадратичной функции является парабола. Свойства функции y = ax2(частный случай) при а > 0. 1. Если х = 0, то y = 0. График функции проходит через начало координат. 2. Если х
0. Графиком квадратичной функции является парабола. Свойства функции y = ax2(частный случай) при а > 0. 1. Если х = 0, то y = 0. График функции проходит через начало координат. 2. Если х ![]() 0, то y > 0. График функции расположен в верхней полуплоскости. 3. График функции симметричен относительно оси Oy. 4. Функция убывает в промежутке (-
0, то y > 0. График функции расположен в верхней полуплоскости. 3. График функции симметричен относительно оси Oy. 4. Функция убывает в промежутке (- ![]() ; 0] и возрастает в промежутке [0; +
; 0] и возрастает в промежутке [0; + ![]() ). 5. Наименьшее значение функция принимает при х = 0. Область значений функции [0; +
). 5. Наименьшее значение функция принимает при х = 0. Область значений функции [0; + ![]() ). Свойства функции y = ax2 при а < 0. 1. Если х = 0, то y = 0. График функции проходит через начало координат. 2. Если х
). Свойства функции y = ax2 при а < 0. 1. Если х = 0, то y = 0. График функции проходит через начало координат. 2. Если х ![]() 0, то y < 0. График функции расположен в нижней полуплоскости. 3. График функции симметричен относительно оси Oy. 4. Функция убывает в промежутке [0; +
0, то y < 0. График функции расположен в нижней полуплоскости. 3. График функции симметричен относительно оси Oy. 4. Функция убывает в промежутке [0; + ![]() ) и возрастает в промежутке (-
) и возрастает в промежутке (- ![]() ; 0]. 5. Наименьшее значение функция принимает при х = 0. Область значений функции (-
; 0]. 5. Наименьшее значение функция принимает при х = 0. Область значений функции (- ![]() ; 0]. И, так, график функции y = ax2 + bx + c есть парабола, вершиной которой является точка (m; n), где m =
; 0]. И, так, график функции y = ax2 + bx + c есть парабола, вершиной которой является точка (m; n), где m = ![]() , n=
, n= ![]() . Осью симметрии параболы служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены вверх, при a < 0 - вниз.
. Осью симметрии параболы служит прямая х = m, параллельная оси y. При а > 0 ветви параболы направлены вверх, при a < 0 - вниз.

Ответ 3
Если переменная у обратно пропорциональна переменной х, то эта зависимость выражается формулой ![]() , где
, где ![]() - коэффициент обратной пропорциональности.
- коэффициент обратной пропорциональности.
- Область определения функции
 - есть множество всех чисел, отличных от нуля, т. е.
- есть множество всех чисел, отличных от нуля, т. е.  .
. - Графиком обратной пропорциональности у=k/x является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой. Если k>0, то ветви гиперболы расположены в I и III координатных четвертях; если же k<.0, то во II и IV координатных четвертях.
- Заметим, что гипербола не имеет общих точек с осями координат, а лишь сколь угодно близко к ним приближается.

№ 4. Опр. Функция, заданная формулой y = ax, где а - некоторое положительное число, не равное еденице, называется показательной. 1. Функция y = ax при а>1 а) область определения - множество всех действительных чисел; б) множество значений - множество всех положительных чисел; в) функция возрастает; г) при х = 0 значение функции равно 1; д) если х > 0, то ax > 1; е) если х < 0, то 0< ax <1; 2. Функция y = ax при 0< а <1 а) область определения - множество всех действительных чисел; б) множество значений - множество всех положительных чисел; в) функция убывает; г) при х = 0 значение функции равно 1; д) если х > 0, то 0< ax <1; е) если х < 0, то ax > 1.

 №5.Опр. Функцию, заданную формулой y = loga x называют логарифмической функцией с основанием а. Свойства функции y = loga x при a>1: а) D(f) = R+; б) E(f) = R; в) функция возрастает; г) если x = 1, то loga x = 0; д) если 0<x<1, то loga x < 0; е) если x > 1, то loga x > 0. Свойства функции y = loga x при 0<a<1: а) D(f) = R+; б) E(f) = R; в) функция убывает; г) если x = 1, то loga x = 0; д) если 0 < x < 1, то loga x > 0; е) если x > 1, то loga x < 0.
№5.Опр. Функцию, заданную формулой y = loga x называют логарифмической функцией с основанием а. Свойства функции y = loga x при a>1: а) D(f) = R+; б) E(f) = R; в) функция возрастает; г) если x = 1, то loga x = 0; д) если 0<x<1, то loga x < 0; е) если x > 1, то loga x > 0. Свойства функции y = loga x при 0<a<1: а) D(f) = R+; б) E(f) = R; в) функция убывает; г) если x = 1, то loga x = 0; д) если 0 < x < 1, то loga x > 0; е) если x > 1, то loga x < 0.
 №6. Опр. Отношение катета прямоугольного треугольника, противолежащего острому углу, к гипотенузе называется синусом этого угла (обозначается sin
№6. Опр. Отношение катета прямоугольного треугольника, противолежащего острому углу, к гипотенузе называется синусом этого угла (обозначается sin ![]() ).
).
- область определения - множество всех действительных чисел;
- множество значений - [-1; 1];
- функция нечетная: sin(-x) = -sin(x) для всех
 ;
; - функция периодическая с наименьшим положительным периодом
 ;
; - sin(x) = 0 при x =
 ;
; - sin(x) > 0 для всех
 ;
; - sin(x) < 0 для всех
 ;
; - функция возрастает на
 ;
; - функция убывает на
 .
.
![]() № 7.Опр. Отношение катета прямоугольного треугольника, прилежащего к острому углу, к гипотенузе называется косинусом этого угла (обозначается cos
№ 7.Опр. Отношение катета прямоугольного треугольника, прилежащего к острому углу, к гипотенузе называется косинусом этого угла (обозначается cos ![]() )
)
- область определения - множество всех действительных чисел;
- множество значений - [-1; 1];
- функция четная: cos(-x) = cos(x) для всех
 ;
; - функция периодическая с наименьшим положительным периодом
 ;
; - cos(x) = 0 при
 ;
; - cos(x) > 0 для всех
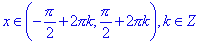 ;
; - cos(x) > 0 для всех
 ;
; - функция возрастает на
 ;
; - функция убывает на

