подставим его в первое и учтем, что

, (4)

В результате получим первое уравнение в следующем виде:

, (5)

Воспользуемся тем, что Y31=0 и преобразуем формулу 5

, (6)

Отсюда получается операторный коэффициент передачи цепи по напряжению

, (7)

где K(p)-операторный коэффициент передачи цепи по напряжению.

Подставим в формулу 6 выражения для Yji, получим:

, (8)

где K(p)-операторный коэффициент передачи цепи по напряжению,

p- оператор Лапласа.

Обозначив в формуле 8 за:

,

Получим операторный коэффициент передачи цепи по напряжению в виде отношения двух полиномов:

, (9)

где K(p)-операторный коэффициент передачи цепи по напряжению

Воспользуемся найденными из формулы 8 коэффициентами и рассчитаем их значения для различных коэффициентов m. Расчёт приведён в приложении 1.

По результатам расчётов составим таблицу коэффициентов полиномов.

Таблица 1

	a1	a0	b1	b0
m1=100	9,028*10-4	4,556	-6*10-4	-6,667
m2=100000	0,88	4,445*103	-0,6	-6.667*103

2. КОМПЛЕКСНО – ЧАСТОТНАЯ ХАРАКТЕРИСТИКА ЦЕПИ

Заменив p на jw, получим комплексный коэффициент передачи цепи по напряжению.

, (10)

где K(jw)-комплексный коэффициент передачи цепи по напряжению,

w- круговая частота, рад/с.

Для нахождения аналитических выражений для АЧХ и ФЧХ коэффициента передачи цепи по напряжению, преобразуем формулу 10 к показательной форме записи и получаем:

Для амплитудно-частотной характеристики:

, (11)

где K(w)-амплитудно-частотная характеристика,

w- круговая частота, рад/с.

Для фазо-частотной характеристики:

, (12)

где Y(w)-амплитудно-фазовая характеристика,

w- круговая частота, рад/с.

3. ГРАФИКИ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЦЕПИ

Построим амплитудно-частотную характеристику цепи для двух значений коэффициента усиления.

Рис. 4

Графики для фазочастотных характеристик для двух значений коэффициента усиления:

Рис.5.

Погрешность АЧХ

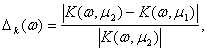
Рис. 4.1.

Погрешность ФЧХ

Рис. 5.1.

4. ПЕРЕХОДНАЯ И ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА ЦЕПИ

Для определения переходной и импульсной характеристик цепи с начала найдём их операторные изображения.

Для переходной характеристики цепи:

, (13)

где g(t)- переходная характеристика,

p-оператор Лапласа,

H(p)- операторная характеристика.

Для импульсной характеристики:

, (14)

где h(t)- импульсная характеристика,

p-оператор Лапласа,

H(p)- операторная характеристика.

(15) (16)

Используя обратное преобразование Лапласа переходим от изображения искомых временных характеристик к оригиналам. 5. ГРАФИКИ ВРЕМЕННЫХ ХАРАКТЕРИСТИК

Воспользуемся формулами (15) и (16), а также значениями коэффициентов, полученных в таб. 1. построим графики импульсной и переходной характеристик для всех значений коэффициентов усиления операционного усилителя.

Переходная характеристика:

Рис. 6.

Импульсная характеристика:

Рис. 7.

6. ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ВРЕМЕНИ ЦЕПИ

Постоянная времени цепи первого порядка равна модулю обратной величины полюса передаточной функции. Полюсами передаточной функции называется все значения аргумента p=poi, при которых знаменатель передаточной функции обращается в ноль. В формуле 9 приравняем знаменатель функции к нулю, в результате получим:

, (17)

где t- постоянная времени цепи, с

Используя формулу 16, рассчитаем значения постоянных времени цепи для всех значений коэффициента усиления операционного усилителя. Расчёт приведён в Приложении 1.

Постоянные времени цепи

Таблица 2

	t, с	t, мкс
m=100	1.982*10-4	19,82
m=100000	1,98*10-4	19,82