Содержание

СОДЕРЖАНИЕ

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ДИСПЕРСИЯ

ФОНДООТДАЧА

ИНДЕКСЫ

ЗАНЯТОСТЬ И БЕЗРАБОТИЦА

ДЕНЕЖНАЯ МАССА

ПРАКТИЧЕСКАЯ ЧАСТЬ

ЗАДАЧА № 1

Условие

Решение

ЗАДАЧА № 2

Условие

Решение

ЗАДАЧА № 3

Условие

Решение

ЗАДАЧА № 4

Условие

Решение

ЗАДАЧА № 5

Условие

Решение

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

Теоретическая часть

Дисперсия

В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трёх видов дисперсий: общей, межгрупповой и внутригрупповой.

§ Общая дисперсия () измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака от общей средней и может быть вычислена как простая дисперсия или как взвешенная дисперсия ;

§ Межгрупповая дисперсия () характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней :

§ Внутригрупповая (частная) дисперсия () отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтённых факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия .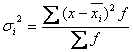

§ На основании внутригрупповой дисперсии по каждой группе, т.е. на основании можно определить общую среднюю из внутригрупповых дисперсий:

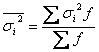
• Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий: . Пользуясь правилом сложения дисперсий, можно всегда определить третью - неизвестную, а также судить о силе влияния группировочного признака.

В статистическом анализе широко используется эмпирический коэффициент детерминации () – показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:

.

Эмпирический коэффициент детерминации показывает долю вариации результативного признака под влиянием факторного признака (остальная часть общей вариации обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице.

Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации:

,

оно показывает тесноту связи между группировочными и результативными признаками.

Эмпирическое корреляционное отношение , как и , может принимать значения от 0 до 1.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:

Фондоотдача

Одним из показателей эффективности использования средств труда является фондоотдача.

Фондоотдача – выпуск продукции в стоимостном выражении на единицу (рубль) стоимости основных производственных фондов, является наиболее общим показателем эффективности использования основных средств.

Она рассчитывается путём деления объёма произведённой в данном периоде продукции () на среднюю за этот период стоимость основных производственных фондов ():

,

где .

Фондоотдача показывает, сколько продукции получено с каждого рубля, вложенного в основные фонды; чем лучше используются основные фонды, тем выше показатель фондоотдачи.

Индексы

Индексом в статистике называют относительный показатель, характеризующий изменение величины какого-либо явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов) во времени, пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом и т.д.)

Основным элементом индексного отношения является индексируемая величина. Индексируемая величина – значение признака статистической совокупности, изменение которой является объектом изучения.