Индекс дефлятора используется для перевода значений стоимостных показателей за отчетный период в стоимостные измерители базисного периода. Для построения индекса дефлятора можно использовать индексы с переменными весами.

Индексы постоянного состава, переменного состава и структурных сдвигов. В тех случаях, когда мы анализируем изменение во времени сравниваемой продукции, мы можем поставить вопрос о том, как в различных условиях (на различных участках) меняются составляющие индекса (цена, физический объем, структура производства или реализации отдельных видов продукции). В связи с этим строятся индексы постоянного состава, переменного состава, структурных сдвигов. Индекс постоянного (фиксированного) состава не учитывает изменение объема продажи продукции на различных рынках в текущем и базисном периодах. Индекс переменного состава используется для характеристики изменения средней цены в текущем и базисном периодах.

Территориальные индексы: в статистике существует необходимость сопоставления уровней экономических явлений в пространстве. Для расчета значений используются территориальные индексы. Для их исчисления соответствующие показатели по всем видам продукции умножаются на количество продукции, произведенной во всей области.

5. Индекс инновационной способности экономики (GCI)

Официальная статистика, как российская, так и зарубежная, представляет не очень много данных о результатах научных исследований. Так, Центр исследований и статистики науки (ЦИСН) публикует только сопоставимые данные о патентной деятельности в России и странах ОЭСР. Коэффициент активности изобретательской деятельности (рассчитывается по количеству патентных заявок в расчете на 10 тыс. жителей) составил в РФ в 2003 г. 1,1, что значительно ниже, чем в странах-лидерах (Япония - 29,1, Корея - 9,7, Германия - 6,2, США - 5,7, Финляндия - 5,1, Швеция - 5,3), но ненамного хуже, чем в таких странах, как Франция, Нидерланды, Канада. Сравнительно низок в России и показатель соотношения поданных за рубежом и национальных заявок.

Современная международная статистика, располагающая большими массивами данных о научно-техническом развитии, активно разрабатывает и постоянно совершенствует методы расчета разнообразных индексов и рейтингов конкурентоспособности, отражающих потенциал и сравнительные преимущества той или иной страны. Разработчики этих рейтингов исходят из того, что основной вектор современной глобальной конкуренции лежит в области динамично меняющихся преимуществ, основанных на научно-технических достижениях и инновациях. Новые технологии и обеспечиваемый ими рост производительности и эффективности позволяют добиваться главного условия национальной и отраслевой конкурентоспособности: производства товаров и услуг, которые соответствуют требованиям мировых рынков, на основе высокой производительности труда и при одновременном повышении реальных доходов населения.

Так, в докладе Всемирного экономического форума (ВЭФ) в 2000 г. в дополнение к публиковавшимся ранее рейтингам по позиции "технология" введен новый индекс конкурентоспособного роста (Growth Competitiveness Index, GCI), который стали называть индексом инновационной способности экономики. Он отражает способность национальной экономики к устойчивому экономическому росту в среднесрочной перспективе (ближайшие пять лет), принимая во внимание текущий уровень экономического развития.

В основе построения индекса GCI - выделение группы стран-лидеров по ключевому, с точки зрения авторов, показателю - количеству патентов, зарегистрированных в стране в расчете на 10 тыс. жителей. Кроме того, в модель включены объемы инновационных инвестиций и их эффективность, а также использование информационных технологий в повседневной жизни граждан (количество мобильных телефонов и компьютеров на душу населения в стране, активность пользователей Интернета и т.д.). Особо учитываются институциональные и макроэкономические условия, содействующие или препятствующие инновационной деятельности.

6. Использование общих индексов в экономическом анализе

Индекс цен исторически является одним из первых экономических индексов. Практически задачи индекса цен в основном сводятся к оценке изменений цен во времени (индексы динамики) или в пространстве (территориальные индексы). Построение системы индексов цен базируется на общеметодологических принципах, согласно которым в ней выделяются индивидуальные, сводные индексы и индексы средних цен (тарифов).

Индивидуальный индекс динамики определяется как отношение цены конкретного i-го товара текущего периода (t) к цене предыдущего периода

(t - 1), т.е.

(4.1)

или к цене одного из периодов динамического ряда, принятого за базу сравнения (0), т.е.

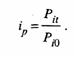(4.2)

Для индивидуальных индексов цен не представляет труда переход от цепных к базисным индексам (свойство круговой сходимости индексов). Обозначим последовательные периоды ряда динамики цен от 0 до п, т.е. t = 0, 1, 2, 3, ., п [2].

Исходя из свойства круговой сходимости индексов величину базисного индекса цен, можно определить как произведение цепных, т.е.

(4.3)

Индивидуальные индексы цен позволяют решать многие практические задачи, но основной задачей является изучение динамики цен разнородной совокупности товаров и услуг. Эта задача решается с помощью сводных индексов, характеризующих среднее изменение цен изучаемой совокупности товаров и услуг.

Сводный (общий) индекс цен относится к числу классических показателей, разработкой которого исследователи занимаются с XVII в.

Наиболее широкое применение в статистической практике получили агрегатные формулы сводных индексов цен, разработанные в середине XVIII в. немецкими учеными Э. Ласпейресом и Г. Пааше.

Индекс Ласпейреса:

(4.4)

Индекс Пааше:

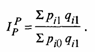(4.5)

Числитель и знаменатель в приведенных индексах состоят из агрегатов, включающих индексируемую величину р и вес q. Различие между индексами Ласпейреса и Пааше заключается в выборе периодов весов. В индексе Ласпейреса берутся веса базисного или предшествующего периода, а в индексе Пааше — текущего периода. При использовании в индексе Ласпейреса весов одного и того же базисного периода в течение длительного времени получают систему сводных индексов цен с постоянными весами, что позволяет учитывать свойство круговой сходимости индексов.

В статистической практике при расчете сводных индексов цен широко применяются различные модификации агрегатных формул, в частности в виде формул среднеарифметических и среднегармонических с использованием индивидуальных индексов (ip).