= 9 500 * 20 + 2 500 * 30 + 1 500 * 15 = 287 500 руб.,

знаменатель индексного отношения

= 7 500 * 20 + 2000 * 30 + 1 000 *15 = 225 000 руб.

Полученные значения подставляем в формулу (3):

или 127,8 %

Применение формулы (3) показывает, что по данному ассортименту товаров в целом прирост физического объёма реализации в текущем периоде составил в среднем 27,8%.

Агрегатный индекс физического объёма товарооборота может определяться посредством использования в качестве соизмерителя индексируемых величин и цен текущего периода .

Агрегатная формула общего индекса будет иметь вид:

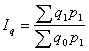(4)

числитель индексного отношения

=9 500 * 25 + 2 500 * 30 + 1 500 * 10 = 327 500 руб.

знаменатель индексного отношения

=7 500 * 25 + 2 000 * 30 + 1 000 * 10 = 257 500 руб.

Полученные значения подставляем в формулу (4):

или 127,2 %

Применение формулы (4) показывает, что по данному ассортименту товаров в целом прирост физического объёма реализации в текущем периоде составил в среднем 27,2%.

3.1.3. Индекс себестоимости

Аналогичным образом производится расчёт индекса себестоимости, при этом сравниваются суммы затрат в производстве в отчётном периоде -

числитель индекса) с суммой затрат в производстве на продукцию отчётного периода по себестоимости базисного периода (- знаменатель).

3.2. Индексы с постоянными и переменными весами

При изучении динамики коммерческой деятельности приходится производить индексные сопоставления более чем за два периода. Поэтому индексные величины могут определяться как на постоянной, так и на переменной базах сравнения. При этом если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Например, сопоставление объёма розничного товарооборота II, III и IV кварталов с I кварталом.

Но если требуется охарактеризовать последовательно изменения изучаемого явления из периода в период, то вычисляются цепные индексы. Например, при изучении объёма розничного товарооборота по кварталам года сопоставляют товарооборот II квартала с I, III — со II и IV — с III кварталом.

В зависимости от задачи исследования и характера исходной информации базисные и цепные индексы исчисляются как индивидуальные, так и общие. Способы расчёта индивидуальных базисных и цепных индексов аналогичны расчёту относительных величин динамики. Общие индексы в зависимости от их вида вычисляются с переменными и постоянными весами — соизмерителями. Используя индексный ряд за несколько периодов, можно получить динамику стоимости продукции и динамику товарооборота в неизменных ценах, т.е. в ценах какого - то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами. Для них действует правило: произведение цепных индексов даёт индекс базисный.

3.3. Средневзвешенные индексы

Помимо агрегатных индексов в статистике применяются средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс.

Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая. Среднеарифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного по формуле средней арифметической, будет равна агрегатному индексу.

3.3.1. Среднеарифметический индекс физического объема

Среднеарифметический индекс физического объема продукции вычисляется по формуле.

3.3.2. Среднеарифметический индекс трудоемкости производства

Среднеарифметический индекс трудоемкости производства продукции определяется следующим образом:

Поскольку , то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции или численность работников в базисном периоде.

3.3.3. Среднеарифметический индекс производительности труда (Струмилина)

В статистике широко известен и среднеарифметический индекс производительности труда. Он носит название индекса Струмилина и определяется следующим образом:

Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности. Среднеарифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей.

3.3.3. Среднегармонический индекс

Среднегармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс себестоимости можно исчислить так:

Таким образом, весами при определении среднегармонического индекса себестоимости являются издержки производства текущего периода, а при расчете индекса цен стоимость продукции этого периода.

4. Базисные и цепные индексы

Цепные индексы: сумма произведений индивидуальных цепных индексов дает базисный индекс за соответствующий период.

Базисные индексы: частное от деления последующего базисного индекса на предыдущий индекс дает нам цепной индекс за соответствующий период.

Преимущество сводных индексов с постоянными весами состоит в том, что их можно сравнивать между собой, а также получать цепные индексы из базисных и наоборот. Для индексов с переменными весами такое правило не сохраняется. С постоянными весами рассчитываются индексы физического объема продукции, а с переменными весами - индексы цен, себестоимости, производительности труда.