Содержание

Содержание. 2

Введение. 3

Глава 1. Теоретические сведения. 3

Коэффициент автокорреляции и его оценка. 3

Автокорреляционные функции. 5

Критерий Дарбина-Уотсона. 7

Глава 2. Примеры практических расчетов с помощью макроса Excel «Автокорреляционная функция» 8

Пример 1. ВВП РФ 8

Пример 2. Импорт. 11

Пример 3. Экспорт. 14

Заключение. 17

Литература. 19

Введение

Периодическая зависимость представляет собой общий тип компонент временного ряда. Можно легко видеть, что каждое наблюдение очень похоже на соседнее; дополнительно, имеется повторяющаяся периодическая составляющая, это означает, что каждое наблюдение также похоже на наблюдение, имевшееся в том же самое время период назад. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i-м элементом ряда и (i-k)-м элементом. Ее можно измерить с помощью автокорреляции (т.е. корреляции между самими членами ряда); k обычно называют лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если ошибка измерения не слишком большая, то периодичность можно определить визуально, рассматривая поведение членов ряда через каждые k временных единиц [7, 153].

Периодические составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции для последовательности лагов из определенного диапазона. На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому что интерес в основном представляют очень сильные[1] автокорреляции [6, 207].

При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой. Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т.д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, (т.е. после взятия разности с лагом 1).

Цель работы:

1. Дать основные теоретические сведения
2. Дать примеры расчета АКФ

Глава 1. Теоретические сведения

Коэффициент автокорреляции и его оценка

Для полной характеристики случайного процесса недостаточно его математического ожидания и дисперсии. Еще в 1927 г. Е.Е.Слуцкий ввел для зависимых наблюдений понятие «связанного ряда»: вероятность возникновения на определенном месте тех или иных конкретных значений зависит от того, какие значения случайная величина уже получила раньше или будет получать позже. Иными словами, существует поле рассеяния пар значений x(t), x(t+k) временного ряда, где k - постоянный интервал или задержка, характеризующее взаимозависимость последующих реализаций процесса от предыдущих. Теснота этой взаимосвязи оценивается коэффициентами автоковариации -

g (k) = E[(x(t) - m)(x(t + k) - m)] -

и автокорреляции

r (k) = E[(x(t) - m)(x(t + k) - m)] / D ,

где m и D - математическое ожидание и дисперсия случайного процесса. Для расчета автоковариации и автокорреляции реальных процессов необходима информация о совместном распределении вероятностей уровней ряда p(x(t1),x(t2)). Однако для стационарных процессов, находящихся в определенном статистическом равновесии, это распределение вероятностей одинаково для всех времен t1, t2 , разделенных одним и тем же интервалом. Поскольку дисперсия стационарного процесса в любой момент времени (как в t, так и в t + k) равна D = g (0), то автокорреляция с задержкой k может быть выражена как [5, 312]

r (k) = g (k) /g (0),

откуда вытекает, что r (0) = 1. В тех же условиях стационарности коэффициент корреляции r (k) между двумя значениями временного ряда зависит лишь от величины временного интервала k и не зависит от самих моментов наблюдений t. [2]

В статистике имеется несколько выборочных оценок теоретических значений автокорреляции r (k) процесса по конечному временному ряду из n наблюдений. Наиболее популярной оценкой является нециклический коэффициент автокорреляции с задержкой k (Андерсон, 1976; Вайну, 1977):

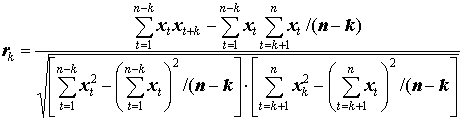
Наиболее важным из различных коэффициентов автокорреляции является первый - r1, измеряющий тесноту связи между уровнями x(1), x(2) , ., x(n -1) и x(2), x(3), ., x(n).

Распределение коэффициентов автокорреляции неизвестно, позтому для оценки их достоверности иногда используют непараметрическую теорию Андерсона (1976), предложившего статистику [4, 112]

t = r1 (n -1)0.5 ,

которая при достаточно большой выборке распределена нормально, имеет нулевую среднюю и дисперсию, равную единице (Тинтнер, 1965).

Автокорреляционные функции

Последовательность коэффициентов корреляции rk, где k = 1, 2, ., n, как функция интервала k между наблюдениями называется автокорреляционной функцией (АКФ).

Вид выборочной автокорреляционной функции тесно связан со структурой ряда.

· Автокорреляционная функция rk для «белого шума», при k >0, также образует стационарный временной ряд со средним значением 0.

· Для стационарного ряда АКФ быстро убывает с ростом k. При наличии отчетливого тренда автокорреляционная функция приобретает характерный вид очень медленно спадающей кривой [3, 268].

· В случае выраженной сезонности в графике АКФ также присутствуют выбросы для запаздываний, кратных периоду сезонности, но эти выбросы могут быть завуалированы присутствием тренда или большой дисперсией случайной компоненты.

Рассмотрим примеры автокорреляционной функции:

• на рис. 1 представлен график АКФ, характеризующегося умеренным трендом и неясно выраженной сезонностью;
• рис. 2 демонстрирует АКФ ряда, характеризующегося феноменальной сезонной детерминантой;
• практически незатухающий график АКФ ряда (рис. 3) свидетельствует о наличии отчетливого тренда.

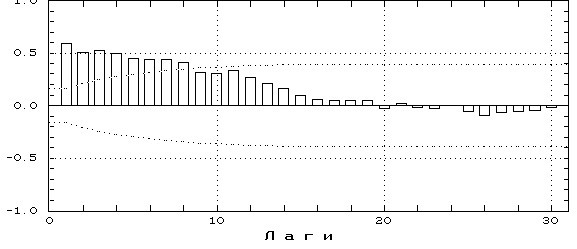
Рис 1.

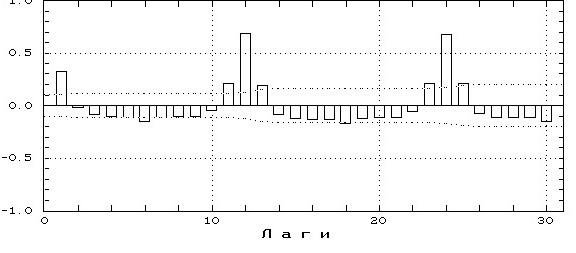
Рис 2.