Разделить сторону квадрата на 11 равных частей

3. Разделить прямоугольник ABCD на 9 равных прямоугольников, не используя измерительных приборов, как на рисунках 1 и 2.

Вариант 2

Прямой угол

1. Методом складывания разделить один из углов квадрата на три равных угла

Геометрия листа произвольной формы

1. Из произвольного листа бумаги получите с помощью сгибов квадрат

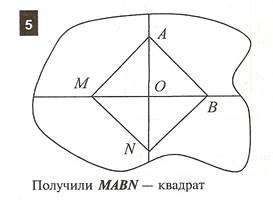
2. Из произвольного листа бумаги получить равносторонний треугольник

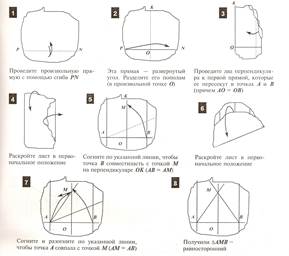
3. На листе бумаги проведены прямая, а также даны центр окружности и некоторая точка на ней (сама окружность не нарисована). Как с помощью перегибаний найти точки пересечения воображаемой окружности с проведенной прямой?

О- центр окружности

А- лежит на окружности

2.2 Задачи на геоплане

Что такое геоплан?

Геоплан представляет собой плоскую поверхность с закрепленными на ней тонкими стержнями, располагающимися в форме квадратной сетки или каким-либо другим способом (в виде окружности, многоугольника). Построение фигур осуществляется на геоплане при помощи эластичных шнуров (резиновых нитей или колец), которые фиксируются между стержнями.

Главное достоинство геоплана состоит в возможности быстрого построения геометрических фигур. При этом не требуются ни бумага с карандашом, ни доска с мелом и не нужно ничего стирать: любую конфигурацию можно быстро изменить или построить заново.

Как строить фигуры на геоплане

Строить (изображать) на геоплане можно различные геометрические фигуры: отрезки, углы, ломаные, треугольники, квадраты, ромбы, прямоугольники, параллелограммы, трапеции, всевозможные многоугольники, а также различные конфигурации, образованные линиями. Можно иллюстрировать или устанавливать свойства геометрический фигур: равенство сторон, углов, площадей, периметров.

Даже незначительные перемещения эластичных нитей по полю геоплана способны изменить (преобразовать) начальную ситуацию: упростить или усложнить ее, рассмотреть частный или более общий случай.

Для чего решать задачи на геоплане

Решение задач на геоплане развивает геометрическую зоркость, умение видеть (распознавать) на чертеже геометрические фигуры или их отдельные элементы, устанавливать их свойства. Работа с геопланом учит наблюдать, анализировать чертеж, проводить опыт, пользоваться здравым смыслом, прикидкой. Все эти умения необходимы каждому человеку. А, кроме того, решать задачи на геоплане это увлекательно!

Как изготовить геоплан самому

Геоплан можно смастерить самому в школьной мастерской или дома. Для этого необходимо подобрать деревянную доску, фанерку или картонку подходящего размера, нанести на нее квадратную сетку и вбить тоненькие гвоздики без шляпок в ее узлах. Желательно, чтобы расстояние между двумя соседними гвоздиками по вертикали или горизонтали было равно 1 дм. В качестве эластичных шнуров можно использовать обычные резиновые жгутики с маленькими петельками или шайбочками на концах, а также тоненькие резиночки со связанными концами (кольца).

При решении задач можно воспользоваться и бумажным прототипом геоплана – обычной ученической тетрадью с наколотой шилом или набитой тонким гвоздиком квадратной сеткой на всех ее листах.

Отрезки

1. Два отрезка, длиной по 5 дм каждый, постройте на геоплане таким образом, чтобы они пересекались в точке, делящей их на четыре отрезка длиной 1 дм, 2 дм, 3 дм, 4дм.

2. На четвертой части геоплана (5х5 дм) разместите десять отрезов длиной 1 дм, 1 дм, 1 дм, 2 дм, 2 дм, 3 дм, 3 дм, 4 дм, 4 дм и 5 дм таким образом, чтобы никакие два из них не имели общей точки.

3. Постройте три отрезка с общим концом так, чтобы длина первого из них равнялась 2 дм, второго – 3 дм, а длина третьего была бы больше длины первого, но меньше длины второго. Найдите два решения.

4. Выберите точку и постройте на вашем геоплане три самых маленьких по длине попарно неравных отрезка с концами в этой точке.

5. Постройте самый короткий и самый длинный отрезки геоплана так, чтобы их общая точка делила один из них на две равные по длине части.

6. Постройте отрезок, являющийся диагональю прямоугольника со сторонами 4 дм и 6 дм. Постройте еще два отрезка, пересекающие первый и разбивающие его на три равные по длине части.

Ломаные

1. Постройте ломаную из пяти звеньев, длиной по 3 дм каждое, так, чтобы расстояние между ее концами равнялось 9 дм; было больше 9 дм; было меньше 9 дм.

2. Из отрезков длиной, равной длине диагонали прямоугольника со сторонами 2 дм и 1 дм, постройте ломаную, состоящую из трех, пяти, семи звеньев, так, чтобы расстояние между ее концами равнялось 1 дм.

3. Постройте ломаную, состоящую из шести звеньев, таким образом, чтобы ее длина была больше 18 дм, но меньше 19 дм.

4. Постройте ломаную в виде буквы русского алфавита, состоящую из двух, трех, четырех звеньев.

5. Постройте ломаную в виде буквы М русского алфавита Переместите одну из ее вершин таким образом, чтобы образовалась ломаная в виде другой буквы русского алфавита.

6. Турист в течении дня несколько раз изменял направление своего движения. До обеда он прошел 4 км на север, затем повернул на восток и двигался 2 км, а далее прошел некоторое расстояние в направлении на северо-восток, больше двух км, но меньше 3 км, и, наконец, км на восток. После обеда он начал двигаться на юг и прошел км, затем повернул на запад и двигался 3 км, а далее он прошел в направлении на юго-запад такое же расстояние, какое он прошел в направлении на северо-восток до обеда. В результате турист оказался в пункте, отстоящем от начальной точки движения на расстоянии 2 км в направлении на восток. Выберите подходящий масштаб и постройте ломаную, изображающую маршрут туриста.

*В данных задачах речь идет лишь о незамкнутой простой ломаной, т.е. о такой, у которой конец последнего звена не совпадает с началом первого и несоседние звенья не пересекаются.

Углы

1. Постройте углы величиной 45, 90, 135, 180 градусов таким образом, чтобы все они имели общую вершину и каждый меньший по величине угол содержался внутри большего.

2. Постройте смежные углы таким образом, чтобы величина одного из них была бы больше 135 градусов.

3. Изобразите на геоплане несколько слов, состоящих из букв русского алфавита, в написании которых встречаются лишь прямые углы.