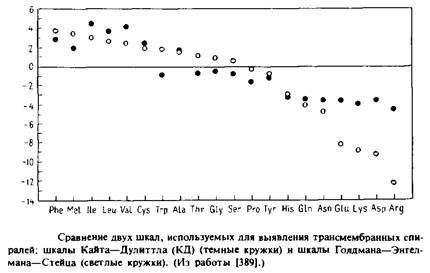
Все сказанное выше показывает, как выигрыш в энергии взаимодействий при переносе а-спирали внутрь бислоя может использоваться для «втягивания» в бислой полярных боковых групп. Например, один остаток аргинина может встроиться в бислой в составе неполярной трансмембранной спирали, если он депротонирован; для этого требуется 16,7 ккал / моль при рН 7,0. Суммарная свободная энергия переноса а-спирали по-прежнему останется отрицательной. Однако ситуация изменится, если в бислой понадобится встроить два аргининовых остатка или если аргинин будет положительно заряжен. Конечно, полярные остатки могут стабилизироваться внутри бислоя благодаря специфическим взаимодействиям, но реально учесть это при расчетах очень трудно. Например, боковые группы серина, цистеина и треонина могут образовывать водородные связи с полипептидным остовом, а кислые и основные остатки могут образовывать ионные пары; появление таких пар возможно, если эти остатки расположены через четыре или пять мономерных единиц друг от друга.

Второй тип шкал, который используется для классификации аминокислот, основан на данных о частоте, с которой аминокислоты действительно встречаются в пронизывающих мембрану сегментах.

При этом эмпирически учитывается гидрофобность, а также многие другие факторы, которые нельзя оценить количественно, как гидрофобность. Недостаток этого полуэмпирического подхода состоит в отсутствии точных данных о границах трансмембранных участков. Тем не менее подобные шкалы могут быть столь же полезны, как и шкалы, основанные на термодинамических параметрах. В качестве примера можно привести шкалу «склонности» к мембране Куна и Лейгха или шкалу «погруженности спирали в мембрану» Рао и Аргоса. Четыре наиболее гидрофобных остатка по шкале Голдмана–Энгелмана–Стейца являются также четырьмя остатками с наивысшим значением параметра по шкале Рао и Аргоса.

На рис. представлены профили трех разных мембранных белков, полученные с использованием различных шкал. При построении этих профилей учитываются средние значения чисел на шкалах, приписываемые каждой аминокислоте в пределах выбранного «окна»; это среднее откладывается относительно номера остатка в полипептиде. Например, если «окно» составляет 19 остатков, значение, приписанное положению 40, будет средним числом на шкале для всех аминокислот от 31 до 49 включительно. Значение, приписанное положению 41, будет средним для остатков с 32 по 50 и т.д. Пики на профиле соответствуют гидрофобным участкам или тем участкам, которые с большей вероятностью образуют трансмембранные спирали. Для построения профиля важен размер окна; большинство кривых на рис. были построены при размере окна в 19 остатков.

Попытаемся проинтерпретировать построенные профили. По шкале Голдмана–Энгелмана–Стейца пики при значениях, близких к нулю, соответствуют трансмембранным спиралям. Значение 1,25 по шкале Кайта–Дулиттла является наименьшим значением, отвечающим известной трансмембранной спирали в L-субъе-динице реакционного центра R. viridis. Во всех трех случаях, представленных на рис. 3.12, профили для субъединиц реакционного центра сходны.

На рис. приведены два профиля для цитохрома Р450 из микросом. Этот белок был выбран потому, что данные о его первичной структуре позволяют высказать предположение о наличии у него восьми трансмембранных спиралей. Однако имеющиеся экспериментальные данные указывают на существование только одного N-koh-цевого якоря в мембране. Как профиль Кайта–Дулиттла, так и профиль Голдмана–Энгелмана–Стейца выявляют N-конце-вой участок, но они указывают и на наличие одного или более дополнительных трансмембранных сегментов, что не соответствует действительности. Отметим, что многие из построенных моделей мембранных белков, которые основываются лишь на данных об аминокислотной последовательности, могут быть некорректными.

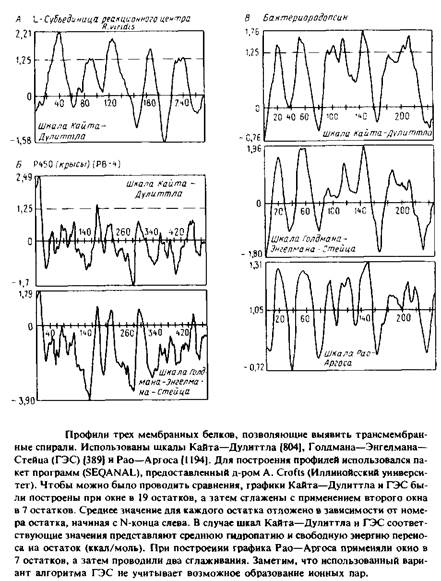
На рис. приведены три профиля для бактериородопсина. Несмотря на их сходство, видны различия в форме пиков, отвечающих семи трансмембранным сегментам. Алгоритм Голдмана–Энгелма-на–Стейца не учитывает стабилизирующего эффекта, связанного с образованием ионной пары из близко расположенных заряженных остатков в пределах одной спирали. С учетом этого фактора разделение между двумя последними спиралями становится более четким.

Одна из проблем, с которыми сталкивается применение всех описанных выше алгоритмов, состоит в том, чтобы исключить гидрофобные сегменты в известных глобулярных белках, не являющиеся трансмембранными, но располагающиеся внутри белка. Однако, когда мы ищем достаточно протяженные участки, эта проблема не возникает.

Отметим, что алгоритмы, используемые для выявления а-спиральных структур в растворимых глобулярных белках, например алгоритм Чоу–Фасмана, непригодны для обнаружения трансмембранных элементов. Эти алгоритмы неприменимы для описания структуры неглобулярных участков, какими являются сегменты, расположенные внутри бислоя.

Алгоритмы, предназначенные для идентификации трансмембранных участков, нельзя использовать в случае сегментов, являющихся вторичными амфифильными структурами или пересекающих мембрану в виде /3-слоя. В первом случае этот участок исключается из рассмотрения из-за наличия в нем полярных остатков, а во втором трансмембранный сегмент оказывается слишком коротким, поскольку для пересечения бислоя необходимо лишь 10–12 аминокислотных остатков в составе /3-структуры. Некоторые алгоритмы предназначались скорее для выявления ^-поворотов, а не самих трансмембранных элементов. Хотя это позволяет избежать некоторых проблем, связанных с выделением различных классов трансмембранных элементов, неясно, насколько приемлемыми они окажутся при более широком их применении.

Способы идентификации вторичных амфифильных структур

Разработано несколько подходов к выявлению вторичной амфифильности или асимметрии в распределении гидрофобных остатков в сегментах полипептидной цепи. Достаточно часто а-спирали и /3-слои в глобулярных белках характеризуются периодичностью в распределении гидрофобных остатков. Использование спирального кольца как качественного показателя не всегда оправданно, необходимы более количественные подходы. Основной из них – это определение периодичности в распределении гидрофобных остатков с помощью методов фурье-преобразования. В качестве примера можно привести гидрофобный момент.

1. Гидрофобный момент. Этот параметр был предложен Эйзенбергом и др. Он определяется как

и представляет собой некую векторную сумму гидрофобности остатков в сегменте из N элементов. Гидрофобность каждого остатка представлена в виде вектора, который характеризуется углом, образуемым боковой цепью и осью полипептидного остова. Для а-спирали 6 = 100°. На рис. 3.9, Б «векторы» гидрофобности представлены в проекции на плоскость спирального кольца, и гидрофобный момент равен их векторной сумме. Гидрофильный остаток представляется вектором с отрицательной направленностью. Для случайной последовательности значение ци в силу случайного распределения гидрофобных остатков будет очень мало. В то же время в пептиде меллитине гидрофобные остатки расположены с одной стороны структуры, а полярные – с другой. Численное значение гидрофобного момента приписывается аминокислоте, находящейся в центре анализируемого сегмента. Следовательно, можно «просканировать» последовательность и приписать каждому положению среднюю гидрофобность, а также найти ^н-