Оценка модели

Симметричная сеть была введена как следующее улучшение, и в качестве примеры был приведен входной импеданс артериального древа организма в целом. Отсюда модно заключить, что в отношении входного импеданса, который "ощущается" левым желудочком, длина сегментов достаточно мала для интересующей нас области частот.

Недостаточное количество данных не позволяет приписать основные локальные значения модуля Юнга различным артериям, представленным в исходной модели. Поэтому в качестве рабочей гипотезы было принято, что среднее значение модуля Юнга можно использовать для всех артерий древа.

Измерения Бергеля, Лиройда и Тейлора показали, что модуль Юнга для различных артерий различен. К тому же модуль Юнга зависит от частоты и величины механических напряжений.

Поводя итог, модно сказать, что с точки зрения влияния на входной импеданс улучшения весьма малы. По-видимому, входной импеданс системы в целом совершенно нечувствителен к рукавному эффекту, симметричной сети или даже к упругому сужению. Также он не зависит практически от периферического сопротивления. [4]

В качестве примера вполне работоспособной модели второго класса с разбиением, близким к оптимальному, можно рассмотреть модель кровообращения, представленную на рисунке 1.

Рис.1. Блок-схема модели кровообращения

Обозначения на рисунке:

А - артерии, В - вены, К - капилляры, Ж - желудочек, П - предсердие, КС - каротидные синусы, ЯВ - яремные вены, ДА - дуга аорты, НА - нисуолящая аорта, ПА - подключичная артерия, ВВ - верхняя полая вена, ГВ и БВ - грудная и брюшная нижние полые вены.

Насосная функция сердца описывается уравнением:

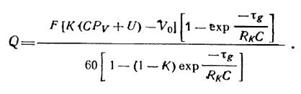
Здесь Q - объемный кровоток на выходе желудочка

F - частота сердечных сокращений

K - сократительная способность сердца

C - диастолическая растяжимость желудочка

Pv - венозное давление на входе сердца

U - ненапряженный объем желудочка при P=0

Vo - свободный член статической аппроксимации Q=Q (Pv).

Экспоненциальные члены описывают динамику процесса с учетом гидравлического сопротивления атриовентрикулярных клапанов и длительности диастолы , причем

где a и b - константы. Объем крови Vi=Vi (t) для i-го участка системы задается уравнением баланса

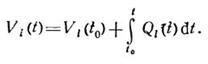
Здесь Qi - алгебраическая сумма по j объемных скоростей кровообмена qij между i-м участком и всеми остальными, причем qij≡0, если j-ый участок непосредственно не сообщается с i-ым. В противном случае принимается, что

где Pi - суммарное давление крови на i-ом участке,

Ri - сопротивление кровотоку на этом участке.

В модели учитывается, что в некоторых периферических венах при падении давления сечение приобретает эллиптическую форму. Для этих сосудов принималось:

А для сосудов верхней половины тела:

Здесь - сопротивление сосуда в условиях, когда его объем равен Ui - ненапряженному объему;

- сопротивление сосуда при горизонтальном положении тела, когда объем сосуда равен .

Зависимость трансмурального давления (давления, обусловленного упругостью сосудистой стенки) от рассматриваемых переменных имеет вид:

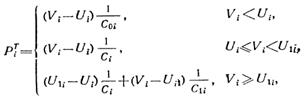
где - объемная податливость сосудов соответственно в области отрицательного, низкого положительного и высоко положительного давлений;

- параметр аппроксимации.

Суммарное давление в i-ом сосуде равно:

Здесь - гидростатическое давление, пропорциональное величине действующей перегрузки и отсчитываемое от выбранного нулевого уровня (обычно от уровня нижней точки тела или уровня сердца);

- давление в тканях, окружающих i-ый участок сосудистого русла:

причем - избыточное давление на поверхности тела в зоне i-го элемента модели;

- внесосудистое давление в тканях в условиях физиологической нормы

ŋ - коэффициент передачи давления, ŋ ≤1.

Эти уравнения полностью описывают биомеханическую модель кровообращения в условиях измененной весомости и перепадов давления по телу. Для учета физиологических компенсаторных реакций в модель дополнительно вводится контур автоматического регулирования давлений крови в зонах аорты и каротидных синусов. В качестве регулируемых параметров приняты частота и сила сердечных сокращений, а также сопротивление, податливость и ненапряженный объем участков сосудистого русла. Отклонение давлений в контролируемых зонах от исходных "нормальных" значений (давления в покое в позе "лежа") приводит к включению схемы пропорционального регулирования вышеперечисленных параметров, причем для каждого из них справедливо уравнение

где Δα - отклонение регулируемого параметра от исходного значения

kα - коэффициент усиления;

Тα - постоянная времени для этого параметра.

Пример использования описанной модели кровообращения для исследования реакций организма на воздействие повышенной весомости приведен на рисунке 2:

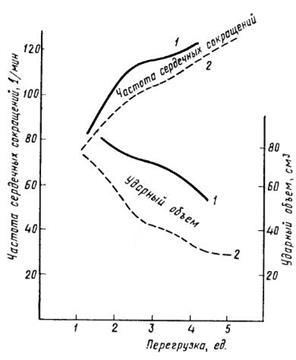
Рис.2. Изменение параметров кровообращения при повышенной весомости. 1 - эксперимент, 2 - расчет.

Видно, что расчетные кривые хорошо отражают качественное изменение физиологических параметров. Практически это означает, что рассмотренный метод расчетной оценки может быть использован для проведения модельных экспериментов по исследованию влияния параметров перегрузки (значение, длительность, скорость нарастания, направление относительно тела человека) и эффективности средств защиты (изменения положения тела, величины, локализации, режима приложения избыточного давления к различным участкам тела). При этом можно ожидать, что полученные результаты будут достаточно надежными, по крайней мере в качественном плане ("лучше","хуже","больше на 30-40%" и т.д.).