Математическое моделирование биосинтеза продуктов метаболизма
 (11),
(11),
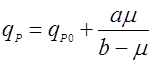 (12).
(12).
 |
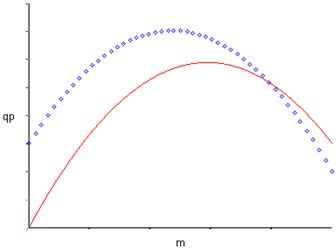
Рис. 2. Форма зависимости qР(m) для уравнений (11) и (12).
Возможны также эмпирические уравнения типа [8,9]:
 |
где а, b, с – эмпирические константы.
Рис. 2. Форма зависимости qР(m) для уравнений (13) и (14).
По аналогии с уравнениями (11) и (12) уравнение (14) начинается, не из 0 по оси ординат, а из некоторой точки a, что означает начало синтеза продукта без роста биомассы.
Субстрат-зависимые модели кинетики биосинтеза продуктов метаболизма.
С точки зрения математики, уравнения, в которых в качестве аргумента выступает m, предполагают, что совсем неважно, каким образом формируется то или иное значение m. Например, величину m можно изменять путем уменьшения концентрации углеродного субстрата или азотного субстрата, или путем снижения температуры или повышения величины рН. Для процессов, связанных только с ростом, возможно скорость биосинтеза при этом будет одинакова. Для несвязанных с ростом процессов небезразлично, каким путем мы будем изменять величину m. Лимитирование углеродом, лимитирование азотом, повышение рН или снижение температуры, давая одно и то же значение скорости роста, могут давать совершенно различные скорости биосинтеза продукта метаболизма. Другими словами, связь между qP и m не имеет строго причинно-следственного характера, а обусловлена влиянием на обе эти кинетические характеристики одних и тех же факторов внешней среды. Для таких процессов необходимо использовать уравнения, которые в качестве аргументов содержат независимо влияющие первичные факторы: концентрация того или иного субстрата, температура или величина рН.
Биосинтез продукта может описываться однофакторными или многофакторными уравнениями. Кроме того, было установлено, что структуры зависимостей qP от S, P, температуры и величины рН аналогичны структурам таких же уравнений для роста биомассы, например: Моно, Андрюса, Перта, Хиншельвуда и т.д. Например, если субстрат влияет на qP по Андрюсу, то имеем [10]:
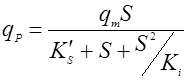 (15),
(15),
где qm – максимальная удельная скорость биосинтеза продукта;
K’S – константа насыщения;
Ki – константа ингибирования продуктом.
Многофакторные зависимости здесь чаще бывают мультипликативными, чем аддитивными. Приведем зависимость мультипликативного [11] и аддитивного влияния концентрации субстрата по механизму Моно:
 (16),
(16),
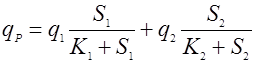 (17).
(17).
Применяются также уравнения с не разделяющимися эффектами факторов, например, типа Контуа [10] или неконкурентного торможения продуктом [5]:
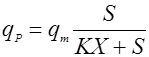 (18),
(18),
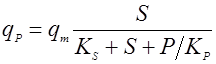 (19).
(19).
К сожалению, невозможно изложить все кинетические зависимости биосинтеза продуктов от первичных факторов в столь короткой работе. Данный материал подробно изложен в монографии [14], в которой приведены не только несколько десятков уравнений, но и произведен их анализ.
Модели, основанные на концепции возраста культуры микроорганизмов.
Для биосинтеза продуктов метаболизма часто бывает недостаточно только благоприятных “внешних” факторов среды. Потому что в биосинтезе участвуют внутриклеточные ферменты микроорганизмов, промежуточные продукты, содержание которых в клетке зависит от предыстории развития культуры. Слишком быстро выросшая культура часто неэффективна с точки зрения биосинтеза продукта. У микробиологов есть выражение “культура ушла в ботву”, что означает биомассы – много, продукта – мало или вообще нет. Однако, учитывать эти внутриклеточные компоненты при моделировании очень проблемно – их трудно измерять и соответственно находить кинетические коэффициенты.
Вместо этого предложены некоторые феноменологические подходы к оценке физиологического состояния микробной биомассы, основанные на оценке возрастного состояния популяции клеток.
Есть несколько подходов для учета возраста культуры. Один из них заключается в определении распределения клеток микроорганизмов по возрастам [12]. Тогда значение удельной скорости биосинтеза продукта можно считать как бы суммой скоростей, даваемых разными возрастными фракциями биомассы:
![]() (20),
(20),
где ΔXi – концентрация биомассы i-ой возрастной группы;
qi – удельная скорость биосинтеза биомассой i-ой возрастной группы.
При этом, вполне возможно, что значения q1, q2, . ,qn не будут одинаковыми: “молодежь” не синтезирует нужный продукт, слишком старые клетки – тоже.
Японским ученым Аибой был предложен более простой подход, использовать для оценки возраста культуры так называемый средний возраст популяции ![]() как параметр, определяющий биосинтетическую активность культуры [13]. Биологически термин вполне понятен – это сумма возрастов всех клеток, деленная на их количество:
как параметр, определяющий биосинтетическую активность культуры [13]. Биологически термин вполне понятен – это сумма возрастов всех клеток, деленная на их количество:
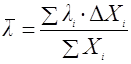 (21),
(21),
где λi – возраст i-ой возрастной группы.
Если последовательно уменьшать поддиапазоны Δt и ΔΧ, доведя их до бесконечно малых dX и dt, то для среднего возраста можно получить интегральную формулу:
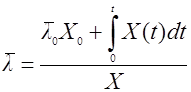 (22),
(22),
где Х0 – начальная концентрация биомассы;
![]() – средний возраст культуры в начальный момент культивирования.
– средний возраст культуры в начальный момент культивирования.
Другим способом упрощения возрастной зависимости является разделение возрастного диапазона клеток на 2 класса – продуктивный (выше некоторого значения) и не продуктивный [14]:
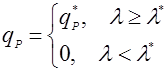 (24),
(24),
где λ* – возраст зрелости;
qP* – удельная скорость биосинтеза клетки, по достижении ею возраста зрелости.
Теперь остается рассмотреть форму зависимости удельной скорости биосинтеза продукта qР от среднего возраста культуры: ![]() .
.
