Содержание

1. Теоретические модели адсорбции полиэлектролитов

1.1 Приближения среднего поля

1.2 Профили распределения

1.3 Влияние полиэлектролитов на отталкивание двойных электрических слоев

1.4 Мостиковое притяжение, обусловленное полиэлектролитами

1.5 Несимметричные системы

1.7 Энергетические мостики

2. Необратимость адсорбции полимеров

3. Измерение адсорбции полимеров

1. Теоретические модели адсорбции полиэлектролитов

Коммерчески доступен широкий спектр разнообразных полиэлектролитов, различающихся структурой и топологией. Одним из простых примеров является полиэтиленимин - положительно заряженный полимер с группами - СН2-СН2-между атомами азота, протонированного при нормальных рН.

В промышленных образцах полиэтиленимин сильно разветвлен и линейными оказываются только димеры и тримеры. Аминокислоты, например глутаминовую кислоту или лизин, можно полимеризовать для получения анионных и катионных полиэлектролитов соответственно. Заряд в этих случаях локализуется в боковых цепях полимера. В первом простом приближении можно предположить, что эти детали не так важны и что главный эффект заключается в том, что в полиэлектролите имеются связанные заряды. Учитывая это предположение, полиэлектролит можно представить моделью "ожерелья" из зарядов, связанных между собой жесткими связями или гармоническими пружинами. Все теории, обсуждаемые ниже, построены на этом предположении.

1.1 Приближения среднего поля

Все известные из литературы теории для полиэлектролитов, адсорбированных на твердых поверхностях, основаны на различных приближениях среднего поля.

Некоторые теории включают решеточное приближение, например теория Брэгга-Вильямса, другие рассматривают непрерывные цепи. Ниже кратко обсуждаются несколько подходов, использующихся для описания адсорбции полиэлектролитов и влияния адсорбции на силы взаимодействия между частицами.

Такие исследования активно развиваются и приведенные ниже сведения не являются исчерпывающими.

Рис.1. Схематическое представление простой модели полиэлектролита, состоящего из заряженных мономерных единиц, связанных между собой упругими пружинами. Пружины моделируют не индивидуальные химические связи, а отражают число связей между заряженными атомами

Теория Схойтенса-Флира {Scheutjens-Fleer). Это наиболее общая теория, разработанная для описания адсорбции полимеров и полиэлектролитов; она оказалась очень хорошей моделью адсорбции полимеров. Теория дает хорошее согласие с экспериментом, но в ней используется много параметров. По выражению авторов: "все результаты и закономерности объяснимы в рамках нашей теории при использовании разумных значений параметров". Одно из преимуществ теории заключается в том, что она применима к полимерам с достаточно длинными цепями. В то же время теория Схойтенса-Флира редко используется для расчета взаимодействий.

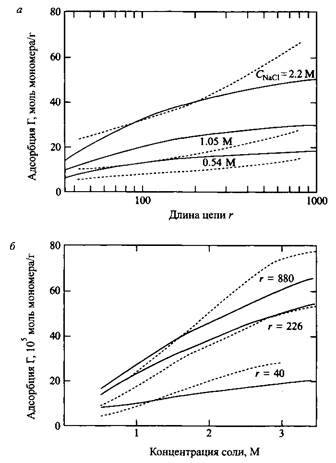
Рис.2. Зависимость адсорбции полиэлектролита от длины цепи г и ионной силы Cs. Сплошные линии представляют оценки по теории Схойтенса-Флира, штриховые линии - экспериментальные результаты

Теория Миклавица-Марцелья {Miklavic-Marcelja). Эта теория рассматривает на поверхности только одиночную цепь и полностью пренебрегает влиянием других адсорбированных цепей. Рассмотрение ограничено короткими цепями. Преимущество этой теории состоит в том, что она позволяет определить исключенный объем в пределах цепи.

Теория адсорбции полиэлектролитов Пуассона-Больцмана. Это прямое распространение уравнения Пуассона-Больцмана на непрерывную цепь. Этот подход, не являясь теорией адсорбции, оказался эффективным для предсказания сил взаимодействия, что было установлено сравнением с результатами, полученными при моделировании методом Монте-Карло. Теория ограничена короткими цепями, результирующее уравнение может быть решено только численно. Теория Подгорника и Офейсдена {Podgornik, Opheusden). Теория рассматривает бесконечно большую непрерывную цепь между двумя заряженными стенками. Справедливость такой модели еще предстоит доказать, в то же время качественно она удовлетворительно описывает некоторые важные физические свойства.

1.2 Профили распределения

Распределение и конфигурация полиэлектролитов с внешней стороны заряженной поверхности, в принципе, можно определить путем исследования рассеяния света, несмотря на сложность интерпретации результатов. Косвенную информацию можно получить из измерений гидродинамического радиуса. Из рис. 16 и 18 видно, что полиэлектролиты адсорбируются на противоположно заряженных поверхностях в плоской конформации, в то время как при адсорбции на одноименно заряженных или нейтральных поверхностях они принимают более вытянутые формы. В первом случае результат можно объяснить электростатическим притяжением между поверхностью и полимерной цепью во втором - отталкиванием между цепями. Введение соли слабо влияет на профиль распределения.

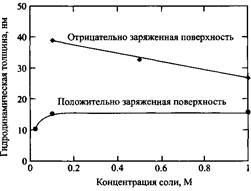
Рис.3. Зависимость гидродинамической толщины адсорбционного слоя полистиролсульфоната на частицах полистирольного латекса от ионной силы раствора

Рис.4. Профили распределения заряженных мономеров полиэлектролитов, адсорбировании концевыми группами на поверхности двух противоположно заряженных стенок, расположенных н расстоянии 60 А. Показана только половина системы, одна из стенок находится при ж = 0. а - Высокая поверхностная плотность заряда; б - низкая плотность поверхностного заряда. Моделировани методом Монте-Карло

1.3 Влияние полиэлектролитов на отталкивание двойных электрических слоев

Добавление гибких полиэлектролитов к заряженным коллоидам оказывает сильное влияние на взаимодействие в системах и может приводить к стабилизации и к дестабилизации дисперсий. Эти эффекты широко используются в раз личных технологиях, например в производстве бумаги, в пищевой промышленности, а также при очистке воды. Биологические системы тоже содержат гибкие полиэлектролиты, например спермин и спермидин, способствующие упаковке ДНК в нативную конформацию и участвующие в процессе коагуляции крови, а также гликолипиды на поверхности мембран.

Рис.18. Профили распределения заряженных мономеров при адсорбции полиэлектролита концевыми группами на поверхности двух стенок: стенки не заряжены, стенки несут заряд, противоположный по знаку заряду полиэлектролита

Взаимодействия в присутствии полиэлектролитов разнообразны, и нельзя ожидать, что на основании уравнения Пуассона-Больцмана можно объяснить все наблюдаемые эффекты. На самом деле во многих случаях системы не подчиняются теории ДЛФО. Рассмотрим несколько идеализированных ситуаций на основе упрощенных моделей полимера, учитывающих два важных свойства - связность и гибкость. Они особенно важны, когда полиэлектролиты взаимодействуют с заряженными поверхностями и модулируют взаимодействия между ними.