Y1,2 = = = 1 i

Y1 = 1– i Y2 = 1 + i

Ответ: {1 + i ; 1– i}

{1– i ; 1 + i}

— Возведем в квадрат

— Возведем в куб

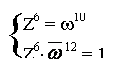w10×12 = 1

w10×10 ×2 = 1

(w×)10×2 = 1

()10×2 = 1

т.к. w = A + B×i

= A – B×i

w× = (A + B×i)·( A – B×i) = A2 – (B×i)2 = A2 + B2 = 2 = w×

т.е. 20·2 = 1

Возьмем модуль от обоих частей последнего уравнения:

20·2 = 1

22 = 1

т.е.

= 1

Тогда из уравнения получим

2 = 1

т.е.

= 1

w1 = 1 w2 = –1

Подставим эти значения в первое уравнение данной системы и найдем численное значение Z

1) w1 = 1

Z6 = 1

1 = 1·( cos(2pk) + i·sin(2pk)), kÎZ

Z = r×(cosj + i×sinj)

r6×(cos6j + i×sin6j) = cos(2pk) + i·sin(2pk), kÎZ

r6 = 1 6j = 2pk

r = 1 j = , kÎZ

Z = cos+ i·sin, kÎZ

k = 0,1,2 .

k = 0

Z1 = cos0+ i×sin0 = 1 + 0 = 1

Z1 = 1

k = 1

Z2 = cos + i·sin = i = i

Z2 =i

k = 2

Z3 = cos+ i·sin = –i

Z3 = –i

k = 3

Z4 = cosp + i·sinp = –1 + 0 = –1

Z4 = –1

k = 4

Z5 = cos + i·sin = –i

Z5 = –i

k = 5

Z6 = cos + i·sin = i

Z6 = i

Ответ: Z1 = 1, Z2 =i, Z3 = –i, Z4 = –1, Z5 = –i, Z6 = i

2) w2 = –1

Z6 = –1

–1 = 1·( cos(p + 2pk) + i·sin(p + 2pk)), kÎZ

Пусть Z = r×(cosj + i×sinj), тогда данное уравнение запишется в виде:

r6×(cos6j + i×sin6j) = cos(p + 2pk) + i·sin(p + 2pk), kÎZ

r6 = 1 6j = p + 2pk

r = 1 j = , kÎZ

Z = cos() + i·sin(), kÎZ

k = 0,1,2 .

k = 0

Z1 = cos + i·sin = i