Число кривых безразличия бесконечно. Это означает, что, как бы ни были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними. Также можно сказать, что каждый инвестор строит график кривых безразличия, представляющих его собственный выбор ожидаемых доходностей и стандартных отклонений. Поэтому инвестор должен определить ожидаемую доходность и стандартное отклонение для каждого потенциального портфеля и нанести их на график в виде кривых безразличия.

Инвесторы, формируя портфель, стремятся максимизировать ожидаемую доходность своих инвестиций при определенном приемлемом для них уровне риска (и наоборот, минимизировать риск при ожидаемом уровне доходности). Портфель, удовлетворяющий этим требованиям, называется эффективным портфелем. Наиболее предпочтительный для инвестора эффективный портфель является оптимальным.

Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает:

1) максимальную ожидаемую доходность для некоторого уровня риска;

2) минимальный риск для некоторого значения ожидаемой доходности.

Набор портфелей, удовлетворяющий этим двум условиям, называется эффективным множеством. Причем особую важность имеют портфели, находящиеся на границе этого множества.

Для измерения риска, связанного с отдельной ценной бумагой, достаточно таких показателей, как вариация или стандартное отклонение (стандартная девиация). Но в случае портфеля мы должны принимать во внимание их взаимный риск, или ковариацию. Ковариация служит для измерения двух основных характеристик:

1) вариации доходов по различным ценным бумагам, входящим в портфель;

2) тенденции доходов этих ценных бумаг, которые могут изменяться в одном или разных направлениях.

Для расчета ковариации с использованием фактических (исторических) данных о доходах ценных бумаг используют следующую формулу:

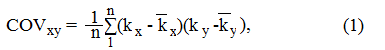
Если в какой-то момент времени доход на акцию х будет ниже среднего и то же наблюдается в отношении акции у, то значение каждого отклонения будет отрицательным, а их произведение — положительным. Аналогично, если одна из переменных х или у ниже средней, а другая — выше, то ковариация будет отрицательной.

В общем виде формула для расчета ковариации будет выглядеть следующим образом:

где pi - вероятность наступления i-гo варианта.

Другим показателем, используемым для анализа портфеля ценных бумаг, является коэффициент корреляции. Напомним, что корреляцией называется тенденция двух переменных менять свои значения взаимосвязанным образом. Эта тенденция измеряется коэффициентом корреляции r, который может варьироваться от +1,0 (когда значения двух переменных изменяются абсолютно синхронно, т.е. изменяются в одном и том же направлении) до -1,0 (когда значения переменных изменяются в точно противоположных направлениях). Нулевой коэффициент корреляции показывает, что изменение одной переменной не зависит от изменения другой.

Коэффициент корреляции (rxy) определяется следующим образом:

где σх, σу - стандартное отклонение доходности ценной бумаги.

Эффективная диверсификация по Марковицу предусматривает объединение ценных бумаг с коэффициентом корреляции менее единицы без существенного снижения доходности по портфелю. В общем, чем ниже коэффициент корреляции ценных бумаг, входящих в портфель, тем менее рискованным будет портфель. Это справедливо независимо от того, насколько рискованными являются эти ценные бумаги, взятые в отдельности, т.е. недостаточно инвестировать просто в как можно большее количество ценных бумаг, нужно уметь правильно выбирать эти ценные бумаги. Такая диверсификация в экономической литературе носит название «чудо диверсификации». Например, инвестирование в акции компаний «Форд» и «Нестле» является рациональной диверсификацией, чего нельзя сказать, например, о вложении средств в ценные бумаги «Форд» и «Фольксваген» (одна отрасль). Одновременные инвестиции в акции компаний «Форд» и «Шелл» также нецелесообразны, поскольку продукция таких компаний взаимосвязана.

Анализ реальной ситуации на биржах ведущих стран показывает, что, как правило, большая часть различных групп акций имеет положительный коэффициент корреляции, хотя, конечно,не на уровне r= +1. Например, на Нью-Йоркской фондовой бирже коэффициент корреляции цен двух случайным образом выбранных групп акций составляет от +0,5 до +0,7.

Следовательно, риск по портфелю, состоящему из двух ценных бумаг, может быть определен так:

где σр - стандартная девиация по портфелю;

dx - доля акции х в портфеле;

dу - доля акции у в портфеле;

σх - стандартная девиация акции х,

σу - стандартная девиация акции у,

r - коэффициент корреляции между акциями х и у.

Переход от портфеля из двух ценных бумаг к портфелю из п бумаг предполагает: во-первых, огромный объем необходимых вычислений и в связи с этим важность использования компьютера и созданного Марковицем алгоритма; во-вторых, увеличение объема исходной информации, необходимой для аналитика. Поэтому на практике чаще используется модель, в основу которой положена корреляция доходов отдельного вида инвестиций с некоторым «индексом», а не со всеми остальными объектами инвестирования, взятыми в отдельности, а также модель ценообразования на капитальные активы.

Модель ценообразования на капитальные активы (САРМ) основывается на том факте, что инвесторы, вкладывающие свои средства в рисковые активы, ожидают некоторого дополнительного дохода, превышающего безрисковую ставку дохода, как компенсацию за риск владения этими активами. Подобное требование описывается техническим термином «неприятие риска» (risk avertion). He принимающие риск инвесторы не обязательно избегают его. Однако они требуют компенсацию в форме дополнительного ожидаемого дохода за принятие риска по инвестициям, доходность по которым не является гарантированной.

Другими словами, САРМ предполагает, что норма дохода по рисковому активу складывается из нормы дохода по безрисковому активу (безрисковой ставки) и премии за риск, которая связана с уровнем риска по данному активу.

Фундаментальное допущение, положенное в основу данной модели, состоит в том, что та часть ожидаемого дохода по ценной бумаге или другому рисковому активу, которая приходится на премию за риск, является функцией связанного с данным активом систематического риска. Поскольку специфический риск достаточно легко можно устранить диверсификацией портфеля, то с точки зрения рынка он не является необходимым. А раз так, то рынок «не вознаграждает» инвестора за этот риск; вознаграждение за риск зависит только от систематического риска.