Сначала построим рекуррентные соотношения для процедур прямой и обратной прогонки, а затем проведем сравнение двух вычислительных схем. Важное различие между двумя формулировками непосредственно следует из определения состояния.

Обозначим количества оставленных и проданных в j-м году овец через xj и yj, соответственно. Положим Zj,=xj+yj. Из условий задачи следует, что

z1=2x0=2k, zj=2xj-1,j=l,2, .,n.

Состояние на этапе j можно описать с помощью переменной zj, которая выражает количество имеющихся к концу этапа j овец для распределения на этапах j+1, j+2, ., n, или с помощью переменной xj, которая выражает количество имеющихся к началу этапа j+1 овец, обусловленное принятыми на этапах 1,2, .,j решениями. Первое определение ориентировано на построение рекуррентного соотношения для процедуры обратной прогонки, тогда как второе определение приводит к использованию алгоритма прямой прогонки.

Алгоритм обратной прогонки

Обозначим через fi(zi) максимальную прибыль, получаемую на этапах j,j+1,…,n, при заданном zj. Рекуррентное соотношение имеет следующий вид:

Заметим, что yj и zj - неотрицательные целые числа. Кроме того, уj (количество овец, проданных в конце периода j) должно быть меньше или равно zj. Верхней границей для значений zj, является величина 2jk (где k- исходный размер стада), которая соответствует отсутствию продажи.

Алгоритм прямой прогонки

Обозначим через gj(xj) максимальную прибыль, получаемую на этапах 1,2, .,j при заданном xj, (где xj— размер стада к началу этапа J+1). Рекуррентное соотношение записывается в следующем виде:

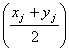- целое.

Сравнение двух формулировок показывает, что представление xj-1 через xj создает более существенные препятствия для вычислений, чем представление zj+1 через zj.

В замене xj-1=(xj+yj)/2 подразумевается целочисленность правой части, тогда как на равенство zj+1=2(zj-yj) такое требование не накладывается. Таким образом в случае процедуры прямой прогонки значения yj и xj, связанные неравенством

Yj <=2jk -Xj,

должны дополнительно удовлетворять условию целочисленности их полусуммы, связанному с видом зависимости хj-1 от xj,. Рассмотренный пример иллюстрирует трудности вычислительного характера, которые обычно возникают при использовании алгоритма прямой прогонки.

2.3 Решение задачи о загрузке

Контрольная работа содержит вопросы по N различным темам. Каждый вопрос типа i имеет вес Vi(i=1,2,…N), а также время, отводимое на ответ Wi. Максимально время, которое может затратить студент на контрольную работу W. Требуется определить максимальное количество баллов (вес), которое может набрать студент за отведенное время W=30. Данные приведены в таблице:

Решить задачу, приведя ее к рекуррентным соотношениям.

Сначала рассмотрим задачу в общей постановке. Если обозначить количество вопросов типа і через ki, то задача принимает следующий вид:

при ограничениях

ki-неотрицательные числа.

Если отбросить требования целочисленности ki, то решение задачи нетрудно найти с помощью симплекс-метода (см. Приложение В). В самом деле, так как остается лишь одно ограничение, базисной будет только одна переменная, и задача сводится к выбору типа і, для которого величина viW/wi принимает максимальное значение. Исходная задача не является задачей линейного программирования, и для ее решения необходимо использовать метод динамического программирования. Следует отметить, что рассматриваемая задача может быть также решена с помощью методов целочисленного программирования.

Каждый из трех основных элементов модели ДП определяется следующим образом.

1. Этап j ставится в соответствии типу j, j=1,2,…,N.

2. Состояние yj на этапе j выражает суммарный вес вопросов, количество ответов на которые приняты на этапах j,j+1,…,N; при этом y1=W и yj=0,1,…,W при j=2,3,…,N.

3. Варианты решения kj на этапе j описываются количеством вопросов типа j. Значение kj заключено в пределах от нуля до [W/wj], где [W/wj]-целая часть числа (W/wj).

Пусть fi(yi)-максимальный суммарный вес вопросов, ответы на которые приняты на этапах j,j+1,…,N при заданном состоянии yj.

Рекуррентное соотношение (для процедуры обратной прогонки) имеет следующий вид:

Заметим, что максимальное допустимое значение kj ограничено величиной [yj/wj]. Это позволяет автоматически исключать все не являющиеся допустимыми варианты при заданном значении переменной состояния yj.

Решение исходной задачи (см. приложении А):

Этап 8.

Этап 7.

Этап 6.

Этап 5.

Этап 4.

Этап 3.

Этап 2.

Этап 1.

Оптимальное решение определяется теперь следующим образом. Из условия W=30 следует, что первый этап решения задачи при y1=30 дает оптимальное решение k1=0, которое означает, что на 0 (нуль) вопросов 1-го типа будут даны ответы. Далее находим: