Высшая математика
Рефераты >> Математика >> Высшая математика

Тогда общее решение заданного неоднородного линейного уравнения имеет вид: .

Ответ:

.

Дополнительно Часть I.

Задание №7. Вопрос №1.

Найти предел: .

Решение:

.

Ответ:

Заданный предел равен .

Задание №9. Вопрос №8.

Найдите уравнение асимптот и постройте их графики:

.

Решение:

1. Область определения данной функции: .

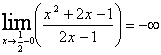2. Т.к. точка не входят в область значений функции, то это точка разрыва, а т.к. и 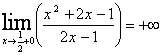, следовательно, уравнение – уравнение вертикальной асимптоты.

3. Уравнения правой и левой наклонных асимптот имеют вид: , где:

Подпись: Рисунок 5. Графики асимптот функции т.к. правая и левая наклонные асимптоты совпадают, то уравнение наклонной

асимптоты имеет вид: .

Для построения графиков асимптот (см. рис. 5), найдем

точки пересечения наклонной асимптоты с осями

координат:

С осью OX: точка,

с осью OY: точка

Ответ:

и – уравнения асимптот заданной функции.

Задание №11. Вопрос №6.

Исходя из определения производной, докажите: .

Решение:

Т.к. по определению производная функции в точке вычисляется по формуле , тогда приращение в точке : .

Следовательно .

Ответ:

.

Задание №15. Вопрос №1.

Найдите пределы, используя правило Лопиталя: .

Решение:

.

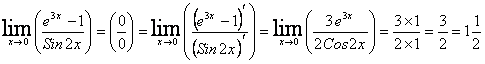Ответ:

Заданный предел равен .

Дополнительно Часть II.

Задание №7. Вопрос №1.

Написать в точке уравнение касательной плоскости к поверхности, заданной уравнением: .

Решение:

Уравнение касательной плоскости к графику функции в точке имеет вид: . Поэтому, продифференцируем заданное уравнение поверхности: . Подставив в полученное уравнение координаты точки вместо значений переменных, и заменив дифференциалы переменных на их приращения, получим:

.

Ответ:

Уравнение касательной плоскости к заданной поверхности в заданной точке имеет вид .

Задание №9. Вопрос №8.

Найти наибольшее и наименьшее значение функции в области: .

Решение:

Т.к. заданная функция дифференцируется в замкнутой ограниченной области, то свое наибольшее/наименьшее значение она достигает или в стационарной точке внутри области дифференцирования, или на границе области.

Найдем стационарные точки заданной функции, для этого решим систему:

, точка не принадлежит заданной области дифференцирования, значит стационарных точек внутри области нет, следовательно, наибольшее/наименьшее значение функцией достигается на границе области дифференцирования. Граница области ограничена окружностями и . Найдем наибольшее/наименьшее значение на границах области дифференцирования. Для этого составим функцию Лагранжа:


Страница: