Высшая математика
Рефераты >> Математика >> Высшая математика

, . Найдем стационарные точки графика функции . Для этого решим систему:

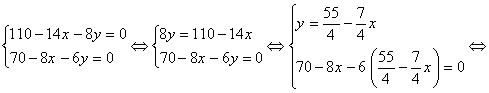
Следовательно - стационарная точка. Проверим ее на экстремум, для этого

введем обозначения: , , ,

тогда , , , . Т.к. > 0, то экстремум есть, а т.к. < 0, то это максимум. Следовательно, при объемах выпуска и , достигается максимальная прибыль равная:

Ответ:

и достигается при объемах выпуска и .

Задание №12. Вопрос №9.

Вычислить неопределенный интеграл:

Решение:

Ответ:

Задание №14. Вопрос №2.

Вычислить несобственный интеграл (или установить его расходимость) .

Решение:

Ответ:

Данный несобственный интеграл – расходящийся.

Задание №15. Вопрос №6.

Решить уравнение

Решение:

. Разделив обе части на , получим . Проинтегрируем полученное уравнение . Представим , как , тогда

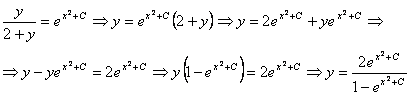
Ответ:

Решением данного уравнения является .

Задание №18. Вопрос №9.

Найти общее решение уравнения:

Решение:

Найдем корни характеристического уравнения: , тогда , следовательно , , тогда

фундаментальную систему решений образуют функции:

,

Т.к. действительные и мнимые решения в отдельности являются решениями уравнения, то в качестве линейно независимых частей решений и , возьмем , , тогда общее решение однородного уравнения будет иметь вид:

Представим правую часть уравнения, как и сравним с выражением, задающим правую часть специального вида:

. Имеем , , тогда т.к. - многочлен второй степени, то общий вид правой части: . Найдем частные решения:

, ,

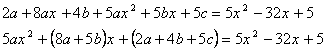
Сравним коэффициенты при слева и справа, найдем , решив систему:

, отсюда .


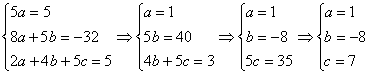Страница: