Следует отметить, что основное уравнение (12.81), полученное для идеализированных условий с допущением, что гср. и Яф.п. являются постоянными величинами, а осадок рассматривается как пористая среда, оказывающая сопротивление ламинарному потоку жидкости в соответствии с законом Дарси. На практике же все осадки и многие перегородки сжимаемы, а это означает, что гср. и R$.u. не являются постоянными, а зависят от ряда факторов, прежде всего от давлений. Кроме того, сжимаемый осадок представляет собой систему сложных сквозных пор и движение жидкости через него не может быть ламинарным. Расход фильтрата, падение давления, удельное сопротивление осадка являются факторами, тесно связанными с изменением пористости осадка, а пористость является очень сложной характеристикой, так как она включает понятие трения жидкой частицы, механическую передачу сил трения от частицы к частице, направление и форму зерен и т. п. Явление сжимаемости осадка в процессе фильтрования впервые было изучено Руттом и Карманом, а впоследствии Теллером и Грассом. Основные положения их теории сводятся к следующему. Удельное сопротивление бесконечно тонкого слоя осадка возрастает от минимума на границе с суспензией до максимума на границе с перегородкой: гср.=ф(рс—Рж), где Рс, Рж — статическое давление суспензии и жидкости.

Удельное сопротивление всего слоя определяется средней интегральной величиной:

(12.85)

При выводе уравнения (12.85) принято, что расход жидкости через слой осадка постоянен, а сопротивление частиц осадка потоку жидкости имеет одну точку опоры, т. е. принято, что удельное сопротивление осадка не зависит от изменения скорости и давления в процессе его образования. Зависимость удельного сопротивления от давления весьма сложна и определяется многими микрофакторами. В связи с этим точное ее математическое описание затруднительно. На практике чаще всего используют эмпирическое уравнение, предложенное Руттом и Карманом:

(12.86)

где S — показатель сжимаемости осадка, изменяющийся в пределах 0<5<1; r' — коэффициент удельного сопротивления осадка.

Общее уравнение фильтрования (12.81) справедливо и для сжимаемых осадков. В этом случае учитывается идеальное сопротивление осадка в соответствии с уравнением (12.86). При этом принимаются во внимание следующие важные упрощения: 1) если сопротивление осадка значительно превосходит сопротивление перегородки, последнее не учитывается; 2) если сопротивление осадка достаточно велико по сравнению с сопротивлением перегородки, то последнее принимается постоянным и учитывается средней величиной, определяемой экспериментально.

Приведенные выше зависимости установлены для одномерного фильтрования, т. е. для плоского фильтровального элемента. Исходя из вышеизложенных зависимостей предложено следующее уравнение, характеризующее процесс фильтрования, на перегородках криволинейной поверхности, таких, как патронные фильтры или так называемое двухмерное фильтрование:

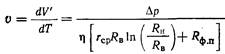(12.87)

где RB — внутренний радиус цилиндрического слоя осадка, м; Ян — наружный радиус цилиндрического слоя осадка, м. Остальные обозначения приведены в (12.81).

Уравнение (12.87) является аналогом основного дифференциального уравнения (12.81) для плоской фильтровальной перегородки, в котором вместо множителя RB• In (RJRB) содержится множитель (V'-m). При R-→∞ предел RB=n(RJRB) равен h и уравнение (12.87) превращается в (12.81). Значения

удельного сопротивления осадка rср. в (12.81) и (12.87) совпадают (хотя эта величина является переменной), т. е. среднееудельное сопротивление осадка не зависит от его формы, что позволяет использовать параметры одномерного фильтрования и rср., полученные из опытов на плоских фильтрах, для расчета двухмерного процесса.

Влияние размерности на процесс фильтрования выражается в том, что при равной толщине осадка скорость фильтрования, отнесенная к единице поверхности фильтрования на цилиндрической поверхности оц (цилиндрическом патроне), будет больше, чем на перегородке с плоской поверхностью Vn:

(12.88)

где Лср — средняя поверхность фильтрования с учетом образующегося осадка, м2; А — поверхность фильтрования плоского фильтрующего элемента, м2; h — толщина слоя осадка, м.

Из уравнения (12.88) вытекает, что производительность фильтров с цилиндрическими фильтрующими элементами на 41 . 80% (в зависимости от режима фильтрования) больше, чем производительность фильтров с плоскими фильтрующими элементами.

Ниже приводятся еще некоторые уравнения, характеризующие процесс двухмерного фильтрования в зависимости от ре^ жима работы фильтра:

при постоянной разности давления Ap=const

(12.89)

при режиме с постоянной скоростью v = const

(12.90)

где 5 — показатель сжимаемости осадка; г' — коэффициент удельного сопротивления осадка; тт — масса твердой фазы. Для определения V и Т предложены зависимости:

Фильтрование при переменных скоростях и разности давления осуществляется центробежным насосом. В этом случае зависимость между скоростями фильтрования v и давлением р, развиваемым центробежным насосом, определяется экспериментально, т. е. опытным путем находят зависимость p=f(v). Для аналитического расчета фильтров предложен приближенный метод, в котором непрерывный процесс при переменных v и р заменяется на процесс, выполняемый сначала при постоянной скорости, а затем при постоянном давлении. Методика расчета заключается в следующем: в начале фильтрования давление насоса р затрачивается на преодоление сопротивления перегородки. Кривая p(j)n=f(Rф) строится по уравнению

где Q — расход фильтрата, м3/с; R0, L — радиус и длина патрона, м. Начальная скорость

(12.92)

Продолжительность фильтрования Rф определяется из уравнения

(12.93)

где рк, рн — давление в конце и в начале фильтрования. Количество фильтрата за время Тф

(12.94)

где А — фильтрующая поверхность; Он — скорость в начале фильтрования.

Скорость ук, соответствующая окончанию фильтрования с постоянной разностью давлений, определяется из соотношения