При огромном количестве теоретической базы по данной тематике, практических работ было немного, т.к. экспериментально доказать, что полимерные цепи адсорбируется изолированно было не возможно.

Главный интерес в исследованиях представляла собой взаимосвязь между поглощающей способностью (масс.%) (А), степенью адсорбции (количество сегментов на одном участке) (Г), различием сегментов в цепях (р) и толщины адсорбционного слоя с такими физическими величинами, как молекулярный вес полимера и параметрами термодинамического взаимодействия между полимером и растворителем и между адсорбирующей полимер поверхностью. Были попытки сформулировать теорию адсорбции полиэлектролитов и теорию отслаивания [5].

В 1955 году гидродинамическим методом была измерена толщина адсорбционного слоя, в 1961 году с помощью инфракрасной спектроскопии впервые определили параметр р, а разработанный метод эллипсометрии в 1963 году позволил одновременно вычислять поглощающая способность и толщину слоя.

До конца 70 годов не было ни одной полноценной теории адсорбции полимеров, а параметры из существующих теорий нельзя было сопоставить с экспериментальными данными.

Широко известно, что свободносочлененная полимерная цепь в идеальном растворителе ведет себя как статистический клубок. При адсорбции такого полимера происходит изменение его конформации. Часть сегментов цепи непосредственно связывается с поверхностью (цепь), а оставшиеся сегменты вытягиваются в растворе (петли и хвосты) (см. рис.1). Если сегмент берет начало на поверхности, то формация «хвост» более выгодна термодинамически, чем формация «петля» [6].

Существует несколько теорий, описывающих адсорбцию неионных полимеров. Первую из них предложил Хов. Он предполагал, что полимерные цепи имеют достаточно большую длину и концевой эффект (формация «хвост») может не рассматриваться, и покрытие поверхности так мало, что взаимодействием между адсорбированными цепями можно пренебречь.

Уравнение изотермы адсорбции выглядит следующим образом:

Na/Sδ = (Nf/V)exp(-λn),

где Na – количество адсорбированного полимера, S – площадь поверхности, δ – толщина первого слоя (слоя «цепь»), Nf – количество неадсорбированного полимера, V – объем растворителя, n – общее количество сегментов в полимерной цепи, λ – константа, определяемая графически исходя из графика ln(Na/Sδ) – ln(Nf/V). В термодинамически хорошем растворителе при уменьшении (-λ) и при увеличении фракции адсорбированных сегментов средний размер петель уменьшается.

Силберберг использовал модель псевдокристаллической решетки при описании адсорбции гибкоцепных полимеров. Он предположил, что если цепь адсорбированного полимера с числом сигментов Р состоит из msi цепей с длинной i и mBi петлей с длинной i, то общее число конфигураций цепи будет равно:

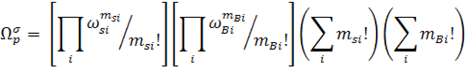
где si и Bi – число возможных конфигураций цепей и петлей соответственно, зависящие от свойств растворителя.

Данная теория не приводит аналитических выражений для изотермы адсорбции и для определения толщины адсорбционного слоя. Силберберг установил, что размер петель в точке θ приблизительно пропорционален квадратному корню из молекулярной массы полимера в широком диапазоне, но необходимо вводить дополнительную константу при больших значениях последних.

Следующая теория носит название теории Шойдженса и Флира. По их представлениям, адсорбированная полимерная цепь также состоит из сегментов, помимо этого в системе присутствуют растворенные молекулы, а адсорбционная поверхность разделена на слои, состоящие из решеток и расположеные параллельно поверхности.

Расчет изотермы адсорбции:

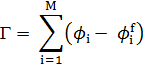
где ϕi – объем фракции адсорбированных цепей, ϕif – объем фракции неадсорбированных цепей в i-ом слое.

Рисунок 2 – Изотерма адсорбции по Шойдженсу и Флиру.

Изотерма адсорбции по Шойдженсу и Флиру аналогична изотерме Лэнгмюра для небольших молекулярных масс, для высоких масс они идентичны. Зависимость Г от молекулярной массы подтверждается теориями Силберберга и Хова.

Шойдженс и Флир вычислили концентрационное распределение петель и хвостовых сегментов, среднеквадратичную толщину адсорбционного слоя, а также длины trains, петель и хвостов.

Дженс рассматривал адсорбцию гибкоцепных полимеров на плоской поверхности из хорошего растворителя с помощью теории отслаивания. В теории отдельно были рассмотрены 3 режима: разбавленный, полуразбавленный и стабилизированный, для каждого из которых были рассчитаны изотермы адсорбции и толщина адсорбционного слоя с использованием химического потенциала.

1.1.2 Факторы, влияющие на адсорбцию полимеров

На адсорбцию полимеров из растворов влияет множество факторов, главные из которых следующие:

1. Влияние поверхности. Экспериментальные данные по адсорбции полимеров подтверждают тот факт, что при варьировании адсорбента величина адсорбции изменяется в широких пределах. Определяющим фактором в данном случае является удельная поверхность адсорбента: чем выше удельная поверхность, тем лучше адсорбция. Было выявлено [7], что образцы с близкой удельной поверхностью, но с разными химическими свойствами, адсорбируют одно и тоже вещество по-разному.

Сравнение адсорбирующей способности поверхностей осложнено тем, что существуют различные способы приготовления одного и того же адсорбента, различные методы ее обработки и т.п. При термической обработке стекла, например, и последующей адсорбции на нем полидиметилсилоксана заметна существенна разница в адсорбции. Из рисунка 3 видно, что адсорбционное взаимодействие адсорбата с 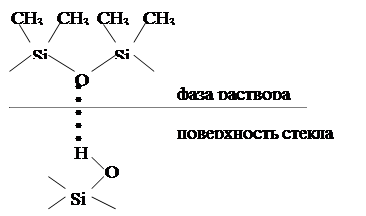обработанным адсорбентом будет намного прочнее, чем с необработанным.

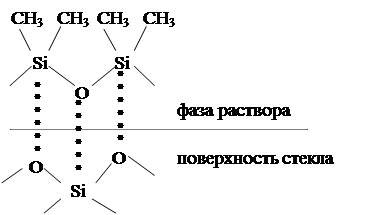
б

Рисунок 3 – Схема адсорбции полидиметилсилоксана на необработанной (а) и обработанной (б) поверхности стекла.

2. Влияние растворителя. Растворитель определяет размеры макромолекулы в растворе, ее ассиметрию и, следовательно, возможную ориентацию молекулы на поверхности, структуру адсорбционного слоя и т.п. Необходимо также принимать во внимание адсорбцию самого растворителя на поверхности, которая мешает сделать правильные выводы об адсорбции макромолекулы. Связь между взаимодействием полимера и растворителя и размерами цепи выражается уравнением Флори-Хаггинса, в основе которого лежит представление об осмотическом давлении статистического клубка макромолекулы [1]:

,

где π – осмотическое давление, с – концентрация раствора, М – молекулярный вес, Аn – вириальные коэффициенты. Второй вириальный коэффициент характеризует энергию взаимодействия молекул полимера и растворителя (и может являться термодинамическим критерием вязкости растворителя наряду с параметром χ из теории Флори-Хаггинса). При уменьшении данного коэффициента происходит уменьшение осмотического давление, что влечет за собой уменьшение размеров макромолекулы и, как следствие, уменьшение вязкости раствора. Таким образом, вязкость связана с термодинамическим качеством растворителя.