зап = 1, реж = 1, ост = 1, пар = 1, ДВ = 1. (20)

Для нахождения нижних доверительных границ надежности

систем воспользуемся общей формулой

, (21)

справедливой для частного случая М = 0.

Соответственно получаем:

· для запуска (N = 39)

Рзап.n = =0.926;

· для стационарного режима (N = 38, т.к. одно испытание с отказом на режиме признанно незачетным)

Рреж.n. ==0.924;

· для останова (N=37, т.к. признаны незачетными два испытания с отказами)

Рзап.n ==0.922.

Для вычисления нижней границы параметрической надежности Рпар используем схему «параметр - поле допуска», приняв допущение о нормальном законе распределения параметра тяги. Предварительно выполним проверку правильности этого допущения с помощью статистического критерия Пирсона (критерия c?). Для этого разобьем диапазон возможных значений тяги на 10 интервалов. Границы интервалов занесем в графы 1 и 2 табл. 6.2. На основе просмотра измерений, приведенных в табл. 6.1, отнесем каждое из них к соответствующему интервалу. Количество измерений, попадающих в интервалы, занесем в графу 4 табл. 6.2. Проведем объединение соседних интервалов, в которых количество попавших измерений оказалось менее четырех (интервалы 1-3 и 8-10) , а уточненное количество попаданий в каждый интервал занесем в графу 7 табл. 6.2. Построим гистограмму распределения измеренных значений параметра тяги (см. рис. 6.1), откладывая по оси абсцисс границы интервалов, а по оси ординат – величины mi/DRi (здесь mi - число измерений, попадающих в

i-й интервал, Ri- длина соответствующего интервала).

Для нахождения теоретических значений частоты попадания в каждый интервал вычислим нормированные значения верхних границ интервалов

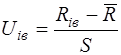(22)

и вероятности получения тяги менее верхней границы

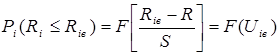. (23)

Значения Uiв и Pi(Ri£ Riв) занесены в графы 8 и 9 соответственно.

Принимаем допущение о нормальном законе распределения тяги двигателя. В качестве параметров нормального закона используем величины

· среднеарифметическое значение тяги

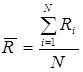; (24)

· среднеквадратичное отклонение тяги

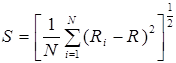. (25)

После необходимых вычислений получаем = 81,99692 S= 0.588026.

Определяем теоретическую вероятность попадания параметра в каждый i-й интервал по формуле

Pi = F[Uiв] - F[U(i-1)в], (26)

в которой F(U) - функция Лапласа, определяемая по таблицам нормального распределения, в зависимости от величины U (см. табл. П 3). Значения вероятностей Pi занесем в графу 10 табл. 6.2, а в графе 11 поместим теоретическое число попаданий в i-й интервал, вычисленное как

miтеор=NPi , (27)

где N - общее число измерений.

Гистограмму теоретического распределения параметра тяги приведем на графике, осуществив предварительно вычисление соответствующих ординат mi/DRi.

Сходство экспериментального и теоретического распределения тяги, приведенных на графике, характеризуется критерием c²

. (28)

Определим критическое значение критерия c²g,k по табл. П 2 в зависимости от g = 0.95 и k= 39-6-2=31: c²g,k = 44,42.

Так найденное значение c² существенно меньше критического значения c²g,k, принятое допущение о нормальном законе распределения тяги следует считать правомерным. Следовательно, нижняя доверительная граница параметрической надежности может быть найдена по формуле

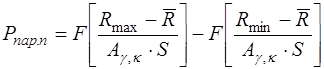, (29)

где Ag,k=1.187 определено по табл. П 2 в зависимости от доверительной вероятности g=0.9 и числа испытаний k=N=40. В нашем случае

.

Так как в табл. П 3 значения функции F(х) приведены только для положительных значений аргумента, воспользуемся формулой (12), тогда

Рпар.n = F(1,985) – 1 + F(1,977) = 0.97558 – 1 + 0.975 = 0.95058.

Минимальное значение нижней доверительной границы надежности Рn(min) полученное для системы, характеризующей останов двигателя (0.922).

Это значение с учетом отсутствия зачетных отказов по всем системам будет характеризовать нижнюю доверительную границу надежности для двигателя в целом. Для обеспечения дальнейшего повышения надежности двигателя необходимо увеличение статистики безотказных испытаний.

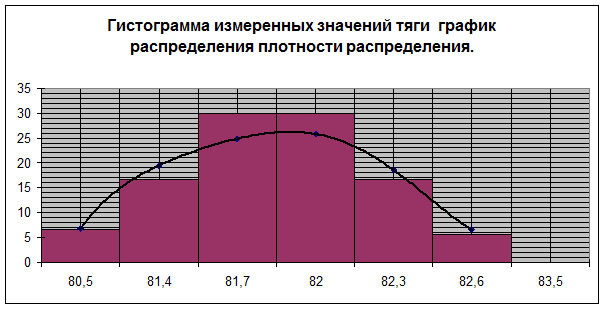
Таблица 6.2