Для возбуждения волн применяют взрыв­ные и ударные источники, которые требуют наблюдений с большой (48—96) кратностью перекрытий.

Обработка данных МОГТ на ЭВМ делится на ряд этапов, каждый из которых заканчи­вается выводом результатов для принятия решения интерпретатором 1) предваритель­ная обработка; 2) определение оптимальных параметров и построение окончательного временного разреза; З) определение скорост­ной модели среды; 4) построение глубинного разреза.

Системы многократных перекрытий состав­ляют в настоящее время основу полевых наблюдений (сбора данных) в МОВ и опреде­ляют развитие метода. Суммирование по ОГТ является одной из главных и эффективных процедур обработки, которые можно реализовать на базе этих систем. Метод ОГТ является основной модификацией МОВ при поисках и разведке нефтяных и газовых месторождений практически во всех сейсмогеологических условиях. Однако результатам суммирования по ОГТ свойственны некоторые ограничения. К ним относятся: а) существен­ное снижение частоты регистрации; б) ослаб­ление свойства локальности МОВ за счет увеличения объема неоднородного простран­ства при больших удалениях от источника, характерных для метода ОГТ и необходимых для подавления многократных волн; в) нало­жение однократных отражений от близких границ вследствие свойственного им сближе­ния осей синфазности при больших удале­ниях от источника; г) чувствительность к бо­ковым волнам, мешающим прослеживанию целевых субгоризонтальных границ вслед­ствие расположения основного максимума пространственной характеристики направлен­ности суммирования в плоскости, перпендикулярной к базе суммирования (профилю).

Указанные ограничения в целом обуслов­ливают тенденцию снижения разрешающей способности МОВ. Учитывая распространенность метода ОГТ, их следует учитывать в конкретных сейсмогеологических условиях.

1.2 Особенности годографа ОГТ.

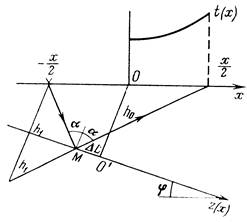
Пусть плоская отражающая граница залегает под углом φ, а покрывающая толща характеризуется скоростью v = const (рис. 2). Обозначим глубину по нормали от центра систему наблюдений до границы раздела (расстояние OO’) через h0. Тогда глубина по нормали, проведенной к границе раздела из пункта взрыва, сдвинутого от центра О системы на расстояние –х/2,

1) годограф ОГТ однократно-отраженной волны для однородной покрывающей среды представляет собой гиперболу с минимумом в точке симметрии (точке ОГТ);

2) с увеличением угла наклона границы раздела крутизна годографа ОГТ и соответственно приращение времени уменьшаются;

3) форма годографа ОГТ не зависит от знака угла наклона границы раздела (эта особенность вытекает из принципа взаимности и является одним из главных свойств симметричной системы взрыв – прибор;

4) для данного t0 годограф ОГТ является функцией только одного параметра – vОГТ, который называется фиктивной скоростью.

Указанные особенности означают, что для аппроксимации наблюденного годографа ОГТ гиперболой необходимо подобрать удовлетворяющее данному t0 значение vОГТ, определяемое по формуле (vОГТ=v/cosφ). Это важное следствие позволяет легко реализовать поиск оси синфазности отраженной волны путем анализа сейсмограммы ОГТ по вееру гипербол, имеющих общее значение t0 и различные vОГТ.

1.3 Интерференционная система ОГТ

В интерференционных системах процедура фильтрации со­стоит в суммировании сейсмических трасс вдоль заданных ли­ний τ(х) с весами, постоянными для каждой трассы. Обычно линии суммирования соответствуют форме годографов полез­ных волн. Взвешенное суммирование колебаний разных трасс yn(t) является частным случаем многоканальной фильтрации, когда операторы индивидуальных фильтров hn(t) пред­ставляют собой δ-функции с амплитудами, равными весовым коэффициентам dn:

(1)

где τm-n – разность времен суммирования колебаний на трассе m, к которой относят получаемый результат, и на трассе n.

Соотношению (1) придадим более простую форму, учиты­вая, что результат не зависит от положения точки т и опре­деляется временными сдвигами трасс τn относительно произ­вольного начала отсчета. Получим несложную формулу, описы­вающую общий алгоритм интерференционных систем,

(2)

Их разновидности отличаются характером изменения весо­вых коэффициентов dn и временных сдвигов τn: те и другие могут быть постоянными или переменными в пространстве, а последние, кроме того, могут изменяться и во времени.

Пусть на сейсмических трассах регистрируется идеально ре­гулярная волна g(t,x) с годографом вступления t(x)=tn:

Подставляя это в (2), получаем выражение, описывающее колебания на выходе интерференционных системы,

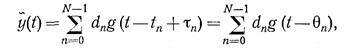
где θn=tn– τn.

Величины θn определяют отклонение годографа волны от заданной линии суммирования. Найдем спектр профильтрованных колебаний:

Если годограф регулярной волны совпадает с линией сумми­рования (θn≡0), то происходит синфазное сложение колебаний. Для этого случая, обозначаемого θ=0, имеем

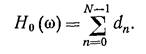
Интерференционные системы строят с целью усиления син­фазно суммируемых волн. Для достижения такого результата необходимо, чтобы H0(ω) было максимальным значением мо­дуля функции Hθ(ω).Чаще всего применяют одинарные интерференционные системы, имеющие для всех каналов равные веса, которые можно считать единичными: dn≡1. В таком случае

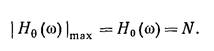
В заключение отметим, что суммирование неплоских волн можно осуществлять с помощью сейсмических источников путем введения соответствующих задержек в моменты возбуждения колебаний. На практике эти виды интерференционных систем реализуют в лабораторном варианте, вводя необходимые сдвиги в записи колебаний от отдельных источников. Сдвиги можно подбирать таким образом, чтобы фронт падающей волны имел форму, оптимальную с точки зрения повышения интенсив­ности волн, отраженных или дифрагированных от локальных участков сейсмогеологического разреза, представляющих осо­бый интерес. Такая методика известна как фокусирование падающей волны.