Страница
3
Сv= =
=![]() =
= ![]() = 0.2638783=0.264.
= 0.2638783=0.264.
Относительная средняя квадратическая ошибка средней многолетней величины годового стока реки за период с 1964 по 1973 гг. (10 лет) равна:
![]() =
= ![]() =
=![]() = 8,3%
= 8,3%
Относительная средняя квадратическая ошибка коэффициента изменчивости Сv при его определении методом моментов равна:
![]() =23,24%.
=23,24%.
Длина ряда считается достаточной для определения Qo и Cv, если ![]()
![]() 5-10%, а
5-10%, а ![]() 10-15%. Величина среднего годового стока при этом условии называется нормой стока. В нашем случае
10-15%. Величина среднего годового стока при этом условии называется нормой стока. В нашем случае ![]() находится в пределах допустимого, а
находится в пределах допустимого, а ![]() больше допустимой ошибки. Значит, ряд наблюдений недостаточный необходимо удлинить его.
больше допустимой ошибки. Значит, ряд наблюдений недостаточный необходимо удлинить его.
3. Определить норму стока при недостатке данных методом гидрологической аналогии.
Река-аналог выбирается по:
– сходству климатических характеристик;
– синхронности колебаний стока во времени;
– однородности рельефа, почвогрунтов, гидрогеологических условий, близкой степени покрытости водосбора лесами и болотами;
– соотношению площадей водосборов, которые не должны отличаться более чем в 10 раз;
– отсутствию факторов, искажающих сток (строительство плотин, изъятие и сброс воды).
Река-аналог должна иметь многолетний период гидрометрических наблюдений для точного определения нормы стока и не менее 6 лет параллельных наблюдений с изучаемой рекой.
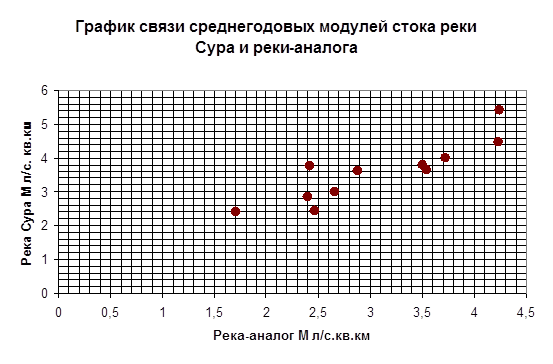
По графику связи Мо равно 7,9 л/с.км2
QO=![]() =
= ![]() =106,02
=106,02
Коэффициент изменчивости годового стока:
Сv=A![]() Cva,
Cva,
где Сv – коэффициент изменчивости стока в расчетном створе;
Cva – в створе реки-аналога;
Моа – среднемноголетняя величина годового стока реки-аналога;
А – тангенс угла наклона графика связи.
В нашем случае:
Сv=1*3,5/3,8*0,27=0,25
Окончательно принимаем Мо=3,8 л/с*км2, QO=106,02 м3/с, Сv=0,25.
4. Построить и проверить кривую обеспеченности годового стока.
В работе требуется построить кривую обеспеченности годового стока, воспользовавшись кривой трехпараметрического гамма-распределения. Для этого необходимо рассчитать три параметра: Qo – среднюю многолетнюю величину (норму) годового стока, Cv и Cs годового стока.
Используя результаты расчетов первой части работы для р. Сура, имеем QO=106,02 м3/с, Сv=0,25.
Для р. Сура принимаем Cs=2Сv=0,50 с последующей проверкой.
Ординаты кривой определяем в зависимости от коэффициента Сv по таблицам, составленным С.Н. Крицким и М.Ф. Менкелем для Cs=2Сv. Для повышения точности кривой необходимо учитывать сотые доли Сv и провести интерполяцию между соседними столбцами цифр.
Ординаты теоретической кривой обеспеченности среднегодовых расходов воды реки Сура с. Кадышево.
Таблица 2
| Обеспеченность, Р% |
0,01 |
0,1 |
1 |
5 |
10 |
25 |
50 |
75 |
90 |
95 |
99 |
99,9 |
| Ординаты кривой |
2,22 |
1,96 |
1,67 |
1,45 |
1,33 |
1,16 |
0,98 |
0,82 |
0,69 |
0,59 |
0,51 | – |
ГРАФИК
Построить кривую обеспеченности на клетчатке вероятностей и проверить ее данные фактических наблюдений.
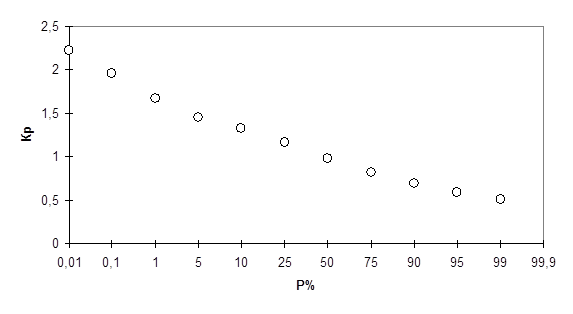
Таблица 3
Данные для проверки теоретической кривой
| № п/п | Модульные коэффициенты по убыванию К | Фактическая обеспеченность Р = | Годы, соответствующие К |
| 1 | 1,52 | 9,09 | 1970 |
| 2 | 1,26 | 18,18 | 1964 |
| 3 | 1,13 | 27,27 | 1968 |
| 4 | 1,06 | 36,36 | 1969 |
| 5 | 1,03 | 45,45 | 1965 |
| 6 | 1,02 | 54,55 | 1971 |
| 7 | 0,84 | 63,64 | 1966 |
| 8 | 0,80 | 72,73 | 1973 |
| 9 | 0,68 | 81,82 | 1967 |
| 10 | 0,67 | 90,91 | 1972 |
