4.5 Разбивка главных точек кривой

Главные точки кривой: начало кривой (НК), конец кривой (КК) и середина кривой (СК) определяются элементами круговой кривой. Элементы круговой кривой – тангенс (Т), кривую (К), биссектрису (Б) и домер (Д) – вычисляют по специальным таблицам. Исходными данными для вычисления элементов круговой кривой является угол поворота трассы и радиус круговой кривой (R) (рисунок 8).

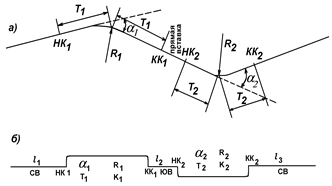
Рисунок 8 – План участка дороги:

а) развёрнутый, б) условный

Расстояние от вершин угла поворота до начала или конца кривой называется дорожным тангенсом, его величину определяют по формуле

. (4.10)

Расстояние от начала до конца кривой по дуге называется длиной этой кривой, которую определяют по формуле

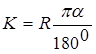. (4.11)

Расстояние от вершин угла поворота до середины кривой к центру поворота называется биссектрисой, определяют по формуле Б = (Sec/2-1).

Разница в длине хода по тангенсам и по кривой называется домером

Д = 2Т – К. (4.15)

Угол поворота вычисляют по измеренному горизонтальному углу теодолитного хода. Величину радиуса бригада принимает самостоятельно. При выборе величины радиуса надо помнить, что между концом данной кривой и началом следующей должна быть прямая вставка длиной не менее 20 метров.

Пример. Измеренный угол теодолитного хода  = 149030’. Угол поворота трассы будет пр = 1800 -  = 180000’ – 1490 = 30030’. Радиус круговой кривой принимаем равным 300 м R = 300 м. По таблицам для разбивки кривых находим значения элементов кривой: Т = 71,79 м; К = 159,70 м; Б = 10,95 м; Д = 3,88 м.

В пикетажный журнал слева от угла поворота записывают величину угла и элементы кривой, а справа – вычисление пикетажного наименования главных точек кривой (рисунок 8).

На местности точки начала и конца кривой определяют рулеткой, откладывая от вершины угла поворота в створе предыдущего и последующего направления линии трассы значение тангенса. Эти точки закрепляют колышками со сторожками, на которых подписывают их пикетажное наименование. Середину кривой определяют при помощи теодолита, установленного в вершине угла поворота. На лимбе горизонтального круга откладывают отсчёт, равный ½ измеренного угла. Вращением лимба визируют на ПК0. Вращением алидады при закреплённом лимбе совмещают нуль лимба с нулём верньера. В створе нового направления, отложив рулеткой значение биссектрисы, находят точку середины кривой. Эту точку, как и предыдущие, закрепляют колышком со сторожком и подписывают её пикетажное наименование. Закрепив на местности главные точки кривой, приступают к разбивке пикетажа по новому направлению. Но так как на углах поворота измерение линий ведется по тангенсам, а действительная длина трассы считается по кривой, то при разбивке пикетажа необходимо учитывать домер. Для этого от вершины угла поворота в створе нового направления откладывают величину домера. В этой точке закрепляют шпильку. Разбивку пикетажа до следующего угла поворота производят от этой шпильки.

Пикеты, находящиеся на тангенсах, выносятся на кривую способом прямоугольных координат. Для этого нужно знать радиус закругления R и Х – расстояние от выносимой точки (пикета или плюсовой точки) до начала кривой. Разбивку кривой ведут от начала и конца кривой к середине. Координаты X и Y берут по радиусу из таблицы кривых Н.Ф. Федорова, где место абсциссы X даётся как разность K-X. В этом случае по тангенсу откладывают длину кривой (K 2K 3K и т.д.) отмеряют назад соответствующие значения K-X. В найденных точках (концах абсцисс) восстанавливают перпендикуляры и откладывают по ним ординаты (Y1, Y2,… Yn), получая точки кривых.

Таким же способом выносят пикеты с линии тангенса на кривую. Длина K определяется как разность пикетажных значений выносимого пикета и начала или (конца) кривой. По таблицам для заданного радиуса по длине кривой определяют K-X и Y, по которым и выносят пикет на кривую, закрепляют «сторожком» с надписью, соответствующей выносимому пикету или плюсу (рисунок 9).

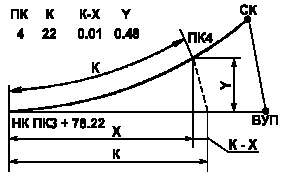
Рисунок 9 – Способ прямоугольных координат

4.6 Составление ведомости прямых и кривых. План трассы

Результаты измерений и вычислений, полученных при проложении на местности трассы, сводятся в ведомость прямых и кривых, которая служит для контроля вычислений, связанных с проектированием трассы (рисунок 10).

Рисунок 10 – План трассы по румбам и длинам

Из журнала нивелирования выписывают величины углов поворота трассы и их пикетажное положение (колонки 2, 3, 4), а также радиусы закруглений (колонка 5).

Элементы кривой (колонки 6, 7, 8, 9) заполняют, пользуясь таблицами для разбивки кривых, входами в которые являются величина угла поворота и радиус закругления (R).

Положение начала и конца кривой записывают в колонки 10, 11.

Длина прямой вставки равна расстоянию между началом второй кривой и концом первой (колонка12).

Расстояние между вершинами углов S (колонка 13) вычисляют как разность пикетажного положения последующей и предыдущей вершин углов поворота плюс домер предыдущей кривой (колонка 9).Азимуты и румбы, колонка 14, 15.

План трассы составляют по данным пикетажной книжки и ведомости прямых и кривых. Трассу наносят по румбам и длинам сторон в масштабе 1:10000 или 1:5000 – для равнинной и холмистой местности и 1:2000 – для горной местности.

Ведомость углов поворотов, прямых и кривых:

4.7 Вычисление азимутов и румбов направлений участков автодороги.

Азимуты последующих направлений вычисляют по формулам

А = Аn-1 + aПРАВ. (4.12)

А = Аn-1 - aЛЕВ., (4.13)

где А – азимут определяемого направления;

Аn-1 – азимут предыдущего направления;

aПРАВ. – угол поворота вправо;

aЛЕВ. – угол поворота влево.

Для нашего примера измеренный азимут начального направления трассы нивелирного хода А1 = 1100, измеренный угол поворота трассы aПРАВ. = 330 И αлев = 290