Из описания конструкций агрегатов и их основных узлов, очевидно, следует, что при существующих габаритах установок и реальных размерах деталей и узлов тракта, по которому проходит гибкая труба, радиусы ее изгиба намного меньше приведенных выше, и поэтому, возникновение пластических деформаций неизбежно. С учетом этого и будем рассматривать вопросы прочности гибкой трубы согласно теории пластичности, поскольку напряжения, действующие в опасном сечении, превышают предел пропорциональности.

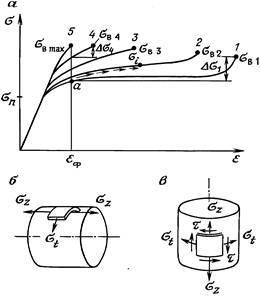
Процесс работы материала КГТ в течение всего срока службы изделия можно охарактеризовать с помощью графиков, приведенных на рис. 18.

Рис. 18. Диаграммы де­формирования материала КГТ в процессе их эксплуатации:

а – видоизменение диаграммы растяжения материала в процессе эксплуатации трубы; 1 – исходная диаграмма; 2 – 4 – диаграммы, соответствую­щие различным стадиям накопления усталости ма­те­риалом трубы; 5 – диаграмма, отражающая момент разрушения трубы; sв1 – sв4 – пределы прочности материала трубы, соответству­ющие различным стадиям; sвmax – предел прочности материала трубы, отража­ю­щий момент ее разрушения; Ds – разность между пределами прочности и текучести; sп – предел пропорциональности материала трубы; eф – максимальная величина деформаций, имеющая место при разрушении трубы; б – напряженное состояние материала трубы в зонах пластического деформирования при ее разматывании и наматывании на барабан; в – то же, в опасном сечении в точке подвеса трубы; нормальные напряжения: st – тангенциальные, обусловленные давлением технологической жидкости в трубах, sz – осевые, обусловленные осевой нагрузкой на трубу и внутренним давлением; t – касательные напряжения, возникающие в результате реактивного крутящего момента при работе забойного двигателя

В начале эксплуатации трубы прочностные и деформационные свойства материала соответствуют кривой 1, представляющей по существу диаграмму идеально пластичного материала. При этом напряжения, возникающие при пластическом деформировании трубы в период ее взаимодействия с барабаном, определяются чисто геометрическими параметрами

sи = Edтр/Dб.

Этой деформации соответствуют напряжения sа в точке а, которые можно считать равными пределу текучести материала новой трубы sт0. При действии внутреннего давления технологической жидкости и продольного усилия натяжения трубы в продольных и поперечных сечениях возникают следующие нормальные напряжения:

меридиональные sm = pжDб/4dтр;

тангенциальные st = pжDб/2dтр;

продольные sп = Pпр/Fтр;

радиальные sr = –pж,

где Fтр – площадь поперечного сечения трубы; Рпр – усилие, растягивающее трубу.

Величиной последних можно пренебречь, так как они на порядок меньше других напряжений. Таким образом, напряженное состояние труб будем считать плоским.

Указанные напряжения действуют на главных площадках, совпадающих с продольным и поперечным сечениями трубы, так как касательные напряжения здесь отсутствуют.

Для расчетов на прочность при сложном напряженном состоянии трубы, изготовленной из пластичного материала, наи­лучшим образом подходит энергетическая теория Хубера–Ми­зеса. Сущность этой теории заключается в том, что в качестве критерия прочности материала, находящегося в сложном напряженном состоянии, может быть принята величина накопленной удельной энергии деформации изменения формы. В технической литературе эта теория иногда называется четвертой. Эквивалентные напряжения sэкв в данном случае определяются, исходя из величин главных напряжений s1, s2, s3, следующим образом:

sэкв = {0,5[(s1 – s2)2 + (s2 – s3)2 + (s3 – s1)2]}1/2.

Эту теорию для прочностных расчетов в основном используют специалисты американских и канадских фирм, производящих гибкие трубы.

С учетом положений теории пластичности определим величину эквивалентных напряжений, используя эту теорию как наиболее удобную для описания процессов образования пластических деформаций,

sэкв = 2–1/2[(s1 – s2)2 + (s2 – s3)2 + (s3 – s1)2]1/2.

Здесь

s1 = sи + st + sп = Edтр/Dб + pжDб/2dтр + Pпр/Fтр;

s2 = sm = pжDб/4dтр;

s3 = 0.

При этом абсолютный запас прочности, выраженный в напряжениях, а не в коэффициенте запаса прочности по ее пределу, может быть определен как

Ds1 = sв1 – sэкв.

Процесс образования трещин в материалах трубы начинается в том случае, если Ds приближается к нулю.

Для гибкой трубы в начальный период эксплуатации значение Ds1 достаточно велико, и действие внутреннего давления технологической жидкости не приводит к образованию трещин.

По мере эксплуатации гибкой трубы она подвергается циклическим нагружениям и происходит наклеп на межкристаллическом уровне. При этом увеличиваются твердость и соответственно прочностные показатели. В процессе накопления наклепа пластические свойства материала ухудшаются, протяженность площадки текучести сокращается, а значение вторичного модуля упругости увеличивается. Этот процесс хорошо отражается на графике функции, положение которого изменяется от горизонтального к наклонному. На рис. 18 приведено семейство линий (1 – 5), соответствующих разным стадиям нагружения гибкой трубы и соответственно разным степеням эффекта наклепа.

Процесс упрочнения материала сопровождается перемещением точки а по вертикали, абсцисса которой eф соответствует величине деформаций при изгибе трубы во время наматывания ее на барабан. При этом величина Dsi = sвi – sэкв все время уменьшается. Это обусловлено тем, что в процессе охрупчивания sвi растет медленнее, чем sт. В конце концов наступает момент, когда нормальные напряжения, возникающие при пластическом деформировании трубы с образованием деформаций eф, становятся равными или близкими к пределу прочности sвi. При этом наличие даже незначительного давления в трубах приводит к образованию микротрещин, которые постепенно распространяются в глубь стенки трубы. Эти трещины, по нашему мнению, должны располагаться в ее поперечной плоскости, совпадающей с площадками, на которых действуют максимальные главные напряжения.

Из сказанного следует, что недопустимо использовать плашки транспортеров с насечкой, поскольку последняя провоцирует образование микротрещин на поверхности гибкой трубы.

Для количественной оценки числа циклов, выдерживаемых гибкой трубой при ее пластическом деформировании и действии внутреннего давления, необходимо знать закономерности изменения прочностных характеристик материала в зависимости от числа циклов нагружения. Подобных данных в обобщенном виде в настоящее время не существует.